0 引言
一般的图像分割方法,多是基于像素的,即根据像素本身的灰度、颜色、纹理等特征进行分割; 根据具体方法不同,又有基于阈值、基于边缘、基于聚类,以及基于图论等许多方法[4,5]。对于遥感图像,不可避免地容易受到各种噪声干扰。而基于像素的方法,除了计算量大、实时性差以外,抗噪性也较差。而基于分裂-合并的分割策略则能有效地克服这些问题。基于分裂-合并的分割算法是从初始分割出发,基于区域特征的相似度,迭代地合并相似的2个相邻区域,直到满足某个代价函数而停止合并。这里涉及到3个方面: ①初始分割,产生的过分割结果直接影响到最终分割结果的质量; ②区域特征提取,所提取特征是后续区域合并的依据; ③区域合并,包括区域的相似度独立和合并准则的确定。学者们从这3方面对合并-分裂算法进行了广泛而深入的研究[6,7,8]。
目前使用最广泛的遥感图像分割方法是eCognition软件中的分形网络演化算法(fractal net evolution approach, FNEA )。该方法是一种多尺度分割方法,通过计算和比较图像光谱和形状的相似性,自下而上的逐层合并对象。但该方法需要手动反复调节尺度、紧致度和异质度等多个参数,才可能得到较好的分割效果[13]。概率密度估计是概率统计和模式识别中基本问题之一,主要分为参数估计和非参数估计。密度估计在图像分割的应用也很广泛,最为著名的是基于非参数估计的均值漂移算法[14,15]; 此外非参数估计还应用于基于阈值的图像分割中[16]; 而基于参数估计的有限混合模型也经常用于图像分割的建模中[17,18]。
本文基于分裂-合并的分割策略,在对图像进行超像素初始分割的基础上,对每个超像素块进行非参数密度估计,并基于估计的密度,重新将超像素块合并聚类,提出一种新的遥感图像分割算法。
1 基于超像素及其最小生成树上Parzen窗密度估计的图像分割算法
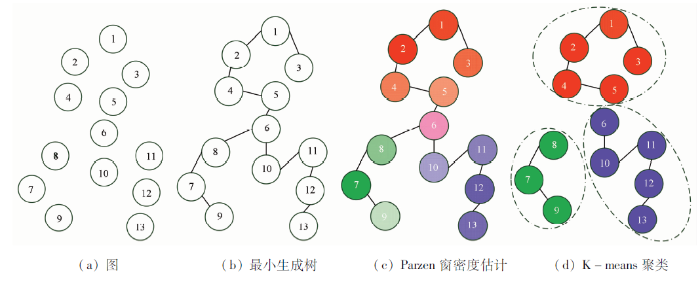
本文方法的主要思路是: 先将图像进行初始超像素分割,把每个超像素块看作图上一个顶点,然后在图的最小生成树上测量顶点间的距离,采用Parzen窗估计方法,在图上估计每个顶点的概率密度,进而寻找不同密度函数的模态进行聚类。其基本原理示意图如图1所示。
图1
图1
图的最小生成树上Parzen窗密度估计的聚类示意图
Fig.1
Cluster based on Parzen windows density estimation on minimum spanning tree
以下先概述SLIC算法,然后给出超像素块的特征提取以及度量方法,再给出基于Parzen窗的密度估计方法,最后详细讨论提出的算法,并给出算法流程图。
1.1 SLIC算法
SLIC超像素分割算法的步骤为[12]:
1)初始化种子点。根据输入图像的像素点个数
2)种子点处理。在种子点的
3)距离测量。将图像转化到Lab颜色空间,分别计算每一个像素点
式中:
4)迭代聚合与连通性处理。重复上述步骤,直到聚类结果稳定,一般迭代十余次即可终止。但可能会存在一些孤立像素或是多连通像素,使用分量连通方法以产生紧致连通的超像素块。
1.2 区域特征的提取与度量
与传统傅里叶方法不同的是,Gabor滤波器可以同时在频率域和空间域都有较好的分辨力,可以方便地在方向和尺度2个参数上进行调整,以符合人类的视觉特性。Gabor滤波器的小波特性使其可以详尽地描述图像纹理特征[19]。
设
对于滤波后的图像Wmn,可得其均值
1.3 Parzen窗密度估计
Parzen窗密度估计(Parzen windows density estimation)又称核密度窗估计,是一种重要的非参数密度估计方法,最早由Parzen[20]提出,它不需要向参数估计方法那样,假定数据分布的概率密度函数参数形式已知,它可以对任意分布的数据作密度估计。现有
式中: 参数
1.4 提出的算法
经过超像素初始分割后,2个超像素块直接的纹理相似度定义为:
式中
根据超像素块之间的纹理特征的相似度,每个顶点(超像素块)
式中
最小生成树是最小权重生成树的简称,它是无向图中包含所有顶点且权值和最小的子图,任意2个顶点之间距离同时蕴含了特征的相似度(权值)和空间的信息[25]。因此,用最小生成树上距离带入Parzen窗密度估计方法中描述顶点(超像素块)的概率密度。
首先,可以用经典的算法,如Krusal算法、Prim算法[26],在以超像素块为顶点的区域邻接图上建立最小生成树; 然后在最小生成树上寻找任意2顶点
式中
可以看到,在Parzen窗密度估计中的距离
最后,将具有相似的概率密度的顶点被认为属于同一模态(类),采用K-means算法完成聚类,得到最终分割结果。整个分割算法流程如图2所示。
图2
图2
提出的多光谱遥感图像分割算法流程
Fig.2
Flow chart of the proposed multispectral remote sensing image segmentation algorithm
2 实验结果及讨论
本文多光谱遥感图像分割的实验平台为2.8 GHz的Pentium4处理器、8 G RAM的计算机,采用软件为MATLAB R2004a。实验1是讨论参数的选择对提出算法分割效果的影响; 实验2和实验3是将提出的算法与eCognition软件中不同参数FNEA算法作对比,验证提出算法的有效性。
为了更有效地评价分割结果,从定性和定量2个方面进行评价。定性即为主观的目视对比判别; 定量则基于手动标注的实际地物边界采用P-R方法[27] 计算,公式分别为:
式中:
2.1 实验分析一
该实验遥感图像选自NWPU VHR-10数据集[28]。图像采集自Google Earth,包括10个类别目标的高分辨率RGB彩色图像和红外图像。实验图像为数据集中178号图像的局部,其中包括船只、水体、植被、建筑物、桥梁等地物目标,图像大小为266像素×385像素,如图3所示。该实验目的是讨论提出算法中的参数设置对分割效果的影响。在提出的算法中主要需要设置3个参数: ①SLIC算法中的S,用于控制超像素块大小; ②Parzen窗带宽h; ③K-means的聚类数。聚类数的选择无疑会对聚类效果有较大影响,许多文献讨论如何自动选择聚类数的问题[29,30],这不是本文主要关注点(实验中发现,只要聚类数在一个大致合理的范围内,分割结果相对稳定,限于篇幅,没有给出实验图像),实验中还是依据经验采用手动给定聚类数。该实验中,所有的聚类数手动选择为5。
图3
表1中给出了参数
表2 实验1中参数S的选取对计算时间的影响
Tab.2
| 参数S | 5 | 20 | 50 |
|---|---|---|---|
| 平均计算时间 | 58.487 6 | 19.783 4 | 14.347 2 |
从表3的P-R定量评价中也可以看出,这2个参数的选择在Precision指标和Recall指标上基本也可以反映出于目视判别解读相同的结论。
表3 实验1的定量评价
Tab.3
| h | S=5 | S=20 | S=50 | |||
|---|---|---|---|---|---|---|
| Precision | Recall | Precision | Recall | Precision | Recall | |
| 0.5 | 0.913 4 | 0.927 2 | 0.914 6 | 0.958 6 | 0.793 4 | 0.828 3 |
| 5 | 0.917 2 | 0.957 3 | 0.916 2 | 0.959 5 | 0.814 1 | 0.841 3 |
| 20 | 0.904 6 | 0.921 7 | 0.920 7 | 0.938 6 | 0.819 2 | 0.839 6 |
| 50 | 0.831 5 | 0.874 6 | 0.742 8 | 0.789 1 | 0.732 5 | 0.749 3 |
2.2 实验分析二
图4
图5
从图4(b)和(c)以及图5(b)和(c)中可以看到,在FNEA方法中,当尺度参数变大,则过分割的问题会得到一定程度克服,但很难完全避免。如图4(b)和(c)中的植被部分,由于植被的光谱异质度较大,产生了明显的过分割,而图5(b)中的水体部分,由于光谱相似度较大,也产生了比较明显的误分割问题。而尺度参数大,又很容易产生欠分割,如图5(c)。同时,图4中建筑物的光谱信息“同谱异物”的情况比较明显,大多数尺度情况下,都容易出现过分割情况。所以,很难找到合理的尺度参数,同时避免以上各种问题的出现。从表4和表5中的定量评价来看,实验2和实验3中分别取比较典型的大小2个不同尺度参数FNEA方法分割结果,其大尺度下的Precision和Recall指标均较小尺度下的有所提高,但非常有限。这也从另一个方面印证了上面的分析。
表4 实验2定量评价
Tab.4
| 指标 | FNEA | 本文方法 | |||
|---|---|---|---|---|---|
| 50 | 150 | S=5 | S=20 | S=30 | |
| Precision | 0.782 9 | 0.798 9 | 0.783 6 | 0.879 8 | 0.884 2 |
| Recall | 0.879 6 | 0.882 7 | 0.870 7 | 0.936 8 | 0.937 1 |
表5 实验3定量评价
Tab.5
指标 | FNEA | 本文方法 | |||
|---|---|---|---|---|---|
| 150 | 200 | S=5 | S=20 | S-30 | |
| Precision | 0.841 1 | 0.856 3 | 0.897 2 | 0.903 7 | 0.912 7 |
| Recall | 0.884 3 | 0.892 7 | 0.912 6 | 0.921 9 | 0.930 5 |
3 结论
针对传统基于像素的遥感图像分割算法易受噪声干扰、计算效率低等缺点,在分裂-合并的框架下,本文提出了一种将超像素和Parzen窗密度估计相结合的遥感图像分割方法,该方法预分割阶段是采用SLIC算法将遥感图像粗分割为超像素,每个超像素块视作图结构中的一个顶点,在图的最小生成树上测量顶点间距离,并采用Parzen窗估计每个顶点密度,然后以这些概率密度为指标对超像素块进行K-means聚类,以达到“融合”目的,得到最终分割结果。提出的方法中有2个方面的主要工作: 一是构建了基于最小生成树的整合了光谱信息、纹理特征和空间信息的距离测量方式; 二是提出了基于图上顶点的Parzen窗密度估计的聚类方法。
为验证提出算法的有效性,在多种多光谱遥感图像上进行分割实验。通过算法中不同参数下的分割结果,以及与不同参数的FNEA算法的分割结果进行比较研究,可以发现提出的算法结果稳定,鲁棒性较好,同时能够克服过分割、误分割和欠分割等问题,得到较好的分割效果。
(责任编辑: 张仙)
参考文献
Object-based change detection in wind storm-damaged forest using high-resolution multispectral images
[J].DOI:10.1080/01431161.2014.930199 URL [本文引用: 1]
Method based on edge constraint and fast marching for road centerline extraction from very high-resolution remote sensing images
[J].DOI:10.3390/rs10060900 URL [本文引用: 1]
Historic land cover change in the agricultural midwest using an object-based approach for classification of high-resolution imagery
[J].DOI:10.1117/1.JRS.7.073506 URL [本文引用: 1]
图像分割方法综述
[J].
Overview of image segmentation metho-ds
[J].
A survey of graph theoretical approaches to image segmentation
[J].DOI:10.1016/j.patcog.2012.09.015 URL [本文引用: 1]
Region-merging method with texture pattern attention for SAR image segmentation
[J].DOI:10.1109/LGRS.8859 URL [本文引用: 1]
An efficient two-stage region merging method for interactive image segmentation
[J].DOI:10.1016/j.compeleceng.2015.09.013 URL [本文引用: 1]
A scalable tile-based framework for region-merging segmentation
[J].DOI:10.1109/TGRS.2015.2422848 URL [本文引用: 1]
高分辨率遥感影像超像素的模糊聚类分割法
[J].
Superpixel segmentation method of high resolution remote sensing image based on fuzzy clustering
[J].
Extract and merge:Superpixel segmentation with regional attributes
[C]//
Superpixel-based spatial-spectral dimension reduction for hyperspectral imagery classification
[J].DOI:10.1016/j.neucom.2019.06.023 URL [本文引用: 1]
SLIC Superpixels compared to state-of-the-art superpixel methods
[J].DOI:10.1109/TPAMI.2012.120 URL [本文引用: 2]
Scale optimization in topographic and hydrographic feature mapping using fractal analysis
[J].
A robust approach toward feature space analysis
[J].DOI:10.1109/34.990134 URL [本文引用: 1]
Color image segmentation using adaptive mean shift and statistical model-based methods
[J].DOI:10.1016/j.camwa.2008.10.053 URL [本文引用: 1]
A novel image thresholding method based on Parzen window estimate
[J].DOI:10.1016/j.patcog.2007.03.029 URL [本文引用: 1]
一种基于高斯混合模型的距离图像分割算法
[J].
A range image segmentation algorithm based on Gaussian mixture model
[J].
可变类空间约束高斯混合模型遥感图像分割
[J].
Remote sensing image segmentation based on spatially constrained Gaussian mixture model with unknown class number
[J].
Selection of Gabor filters for improved texture feature extraction
[C]//
On estimation of a probability density function and mode
[J].DOI:10.1214/aoms/1177704472 URL [本文引用: 1]
Multivariate density estimation:Theory,practice,and visualization
[M].
A brief survey of bandwidth selection for density estimation
[J].DOI:10.1080/01621459.1996.10476701 URL [本文引用: 1]
Fast optimal bandwidth selection for kernel density estimation
[C]//
Non-asymptotic bandwidth selection for density estimation of discrete data
[J].DOI:10.1007/s11009-007-9057-z URL [本文引用: 4]
Toward objective evaluation of image segmentation algorithms
[J].Unsupervised image segmentation is an important component in many image understanding algorithms and practical vision systems. However, evaluation of segmentation algorithms thus far has been largely subjective, leaving a system designer to judge the effectiveness of a technique based only on intuition and results in the form of a few example segmented images. This is largely due to image segmentation being an ill-defined problem-there is no unique ground-truth segmentation of an image against which the output of an algorithm may be compared. This paper demonstrates how a recently proposed measure of similarity, the Normalized Probabilistic Rand (NPR) index, can be used to perform a quantitative comparison between image segmentation algorithms using a hand-labeled set of ground-truth segmentations. We show that the measure allows principled comparisons between segmentations created by different algorithms, as well as segmentations on different images. We outline a procedure for algorithm evaluation through an example evaluation of some familiar algorithms-the mean-shift-based algorithm, an efficient graph-based segmentation algorithm, a hybrid algorithm that combines the strengths of both methods, and expectation maximization. Results are presented on the 300 images in the publicly available Berkeley Segmentation Data Set.
Learning rotation-invariant convolutional neural networks for object detection in VHR optical remote sensing images
[J].DOI:10.1109/TGRS.2016.2601622 URL [本文引用: 2]
Selection of the number of clusters via the bootstrap method
[J].DOI:10.1016/j.csda.2011.09.003 URL [本文引用: 1]
Estimating the number of clusters via a corrected clustering instability
[J].