自然资源遥感, 2022, 34(3): 129-137 doi: 10.6046/zrzyyg.2021237

技术应用

机载LiDAR在红树林林分平均高估算中的应用

邓静雯,1, 田义超,1,2, 张强1, 陶进1,3, 张亚丽1, 黄升光3

1.北部湾大学资源与环境学院,钦州 535000

2.北部湾大学广西北部湾海洋灾害研究重点实验室,钦州 535000

3.北部湾大学海洋地理信息资源开发利用重点实验室,钦州 535000

Application of airborne LiDAR in the estimation of the mean height of mangrove stand

DENG Jingwen,1, TIAN Yichao,1,2, ZHANG Qiang1, TAO Jin1,3, ZHANG Yali1, HUANG Shengguang3

1. Collage of Resources and Environment, Beibu Gulf University, Qinzhou 535000, China

2. Guangxi Key Laboratory of Marine Disaster in the Beibu Gulf, Beibu Gulf University, Qinzhou 535000, China

3. Key Laboratory of Marine Geographic Information Resources Development and Utilization, Beibu Gulf University, Qinzhou 535000, China

通讯作者: 田义超(1986-),男,博士,副教授,主要从事资源环境遥感及海岸带生态环境监测研究。Email:tianyichao1314@yeah.net。

责任编辑: 陈理

收稿日期: 2021-07-28   修回日期: 2021-10-19  

基金资助: 国家自然科学基金项目“桂西南峰丛洼地流域生态系统服务权衡关系及其驱动机制”(42061020)
广西创新驱动发展专项项目“海岸双频激光LiDAR探测仪产品开发与应用示范”(AA18118038)
广西科技基地和人才项目“广西钦州湾红树林岛群生态系统健康评价及应用示范”(2019AC20088)
广西壮族自治区大学生创新创业训练项目“基于激光雷达数据的红树林地上生物量与碳储量反演”(202011607186)

Received: 2021-07-28   Revised: 2021-10-19  

作者简介 About authors

邓静雯(1999-),女,学士,主要从事遥感信息应用研究。Email: 1687606800@qq.com。

摘要

构建基于激光雷达(light detection and ranging,LiDAR)数据的林分平均高反演模型可为无瓣海桑长势的动态监测提供技术支撑。以北部湾茅尾海无瓣海桑红树林湿地为对象,基于机载LiDAR提取的高度和强度参数变量,借助决定系数R2、均方根误差RMSE、赤池信息准则AIC和贝叶斯信息准则BIC指标对随机森林、支持向量机以及神经网络3种模型进行了优选,在最优模型的支持下估算了研究区的红树林平均高及其空间分布状况。结果表明,研究区无瓣海桑的林分平均高介于3.90~11.58 m之间,其中树高较高、胸径较大的无瓣海桑主要分布在潮沟附近以及研究区中部。在估算无瓣海桑的林分平均高时,贡献率最大的是样方点云高度最大值,其次是75%~99%分位数高度。随机森林回归模型在估测林分平均高模型中的精度最高(R2=0.938 1,RMSE=0.58 m,AIC=80.50和BIC=49.05); 支持向量机模型次之,该模型在测试阶段的R2为0.766 5,RMSE为1.27 m; 神经网络模型的拟合效果最差。总体而言,随机森林模型是研究区无瓣海桑林分平均高反演的最优模型。

关键词： 无瓣海桑; 支持向量机; 神经网络; 随机森林; 林分平均高

Abstract

This study constructed a stand mean height inversion model based on LiDAR data, aiming to provide dynamic monitoring of the growth of Sonneratia apetala. Taking the mangrove wetland of Sonneratia apetala in the Maowei Sea of Beibu Gulf as the study object and based on the height and intensity parameters extracted using airborne LiDAR data, this study compared three models, namely random forest, support vector machine, and neural network, based on the coefficient of determination (R2), root mean square error (RMSE), Akachi information criterion (AIC), and Bayesian information criterion (BIC) and then estimated the mean height and spatial distribution of Mangrove in the study area using the optimal model. The results are as follows. The stand mean height of Sonneratia apetala in the study area is 3.90~11.58 m, and Sonneratia apetala with a higher tree height and a larger diameter at breast height is mainly distributed near the tidal trench and the middle part of the study area. In the estimation of the stand mean height of Sonneratia apetala, the maximum percentile height (hmax) had the highest contribution rate, followed by 75%~99% percentile height. The random forest regression model yielded the highest precision (R2=0.938 1,RMSE=0.58 m,AIC=80.50, and BIC=49.05), followed by the support vector machine model (R2 = 0.766 5 and RMSE = 1.27 m in the test stage), and the neural network regression model yielded the worst fitting effects. Overall, the random forest model is the optimal model for the inversion of the stand mean height of Sonneratia apetala in the study area.

Keywords： Sonneratia apetala; support vector machine; neural network; random forest; stand mean height

PDF (7423KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

邓静雯, 田义超, 张强, 陶进, 张亚丽, 黄升光. 机载LiDAR在红树林林分平均高估算中的应用[J]. 自然资源遥感, 2022, 34(3): 129-137 doi:10.6046/zrzyyg.2021237

DENG Jingwen, TIAN Yichao, ZHANG Qiang, TAO Jin, ZHANG Yali, HUANG Shengguang. Application of airborne LiDAR in the estimation of the mean height of mangrove stand[J]. Remote Sensing for Land & Resources, 2022, 34(3): 129-137 doi:10.6046/zrzyyg.2021237

0 引言

红树林群落与其所在的滨海盐生沼泽湿地相互作用形成了红树林生态系统。红树林生态系统是全球最具特色的湿地生态系统,同时具备海洋生态及陆地生态的特性,具有强大的生态防护功能。林分平均高是红树林湿地生态系统模型的一个重要输入参数,是研究红树林碳储量的重要指标之一,也是估算各种红树林参数的基础。因此,采用定量化方法快速、准确地获取红树林林分平均高信息成为了近年来红树林结构参数研究的热点。

人工实地调查在林分平均高调查时费时费力,且调查效率低下。随着遥感技术的日益成熟,遥感技术已成功应用于大尺度森林制图和灾害监测等领域,效率得到了大幅度的提高,但森林高度、生物量等森林结构参数是传统光学遥感无法解决的,而激光雷达(light detection and ranging,LiDAR)技术可以获取森林的结构参数信息[1]。LiDAR是传感器发出激光信号,检测目标物体的位置,接收反射信号从而测量传感器与目标物体之间距离的一种新技术。近几十年来,国内外相关学者在激光点云森林结构参数反演算法方面做了大量的研究, 促进了LiDAR技术在林业方面的发展。其中,Næsset等[2]、Andersen等[3]、焦义涛等[4]、洪奕丰等[5]学者基于机载 LiDAR点云数据,采用线性回归模型对不同区域的森林高度和生物量进行了估算。线性回归模型比较适用于建模目标之间关系相对简单且数据量不大的情况,这类线性回归模型虽然快速简单,但要求建模数据必须满足独立性、线性、正态性以及方差齐性等要求。

相对而言,随机森林、支持向量机以及人工神经网络等算法在构建复杂非线性森林参数估算模型中具有更大优势。如Li等[6]和Monnet等[7]基于机载 LiDAR点云数据,在支持向量机模型的支持下对不同研究区的生物量进行估计,结果显示估测精度较好; 鲁林等[8]和赵勋等[9]基于LiDAR点云数据,采用随机森林算法分别对福建省朱溪河流域的松树以及广西壮族自治区国有高峰林场的人工林林分平均高进行了估算,结果显示林分平均高与实测值具有显著的相关性,其相关系数均超过0.94。但是红树林生长在海岸滩涂地带,人们很难进入其根系繁茂的内部进行测量。虽然国外已有诸多学者对LiDAR反演红树林植被参数的算法开展了深入的研究,但国内学者在这方面的研究较少,仅有少量开展过红树林生物量方面的研究[10-11]。迄今为止,采用机载LiDAR点云对红树林林分平均高方面的研究匮乏。因此,为了支持红树林的恢复、保护和可持续管理,需要采用一种快速高效的模型来评估红树林的林分平均高。而基于机载LiDAR点云数据,采用机器学习算法为红树林林分平均高的估算提供了便捷的技术手段。

无瓣海桑(Sonneratia apetala)天然分布于马来西亚、孟加拉国等国[12],2002年广西钦州市为了加快红树林恢复,从广东湛江市引进了无瓣海桑幼苗进行造林试验。在近年营造的作用下,无瓣海桑迅速占领了适宜的林地,甚至入侵了原生红树林群落[13]。这些入侵的无瓣海桑挤占了原有的本土红树林生长空间,对当地的红树林树种生长造成了一定的影响,但是入侵的无瓣海桑高度如何,目前尚未有定量化的评估数据。鉴于此,基于北部湾茅尾海康熙岭片区的LiDAR点云数据,借助相关数理分析指标对随机森林、支持向量机以及神经网络3种模型进行了优选,在最优模型的支持下估算了研究区的红树林平均高及其空间分布状况,研究方法可为今后该地区无瓣海桑长势的动态监测提供有力的技术支撑。

1 研究区概况

研究区位于北部湾茅尾海康熙岭片区,介于N21°51'26″~21°51'42″,E108°29'27″~108°29'43″之间,该片区属于亚热带季风气候,太阳辐射强,季风环流明显。夏长冬暖,夏季时长有6个月之多,全年平均气温在22 ℃左右,其年均降雨量为1 658 mm,年总日照为1 673 h[14]。钦州市的海水温度、海水盐度、土壤及沉积物,为红树林的生长提供了有力的条件,本次主要研究树种为一种外来木本植物——无瓣海桑(Sonneratia apetala),据当地渔民的调查可知,研究区的无瓣海桑扩散方向如图1黄色箭头所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   研究区红树林地理位置

Fig.1   Location of mangrove in the research area


2 数据来源与研究方法

2.1 数据来源

2.1.1 地面实测样地数据获取

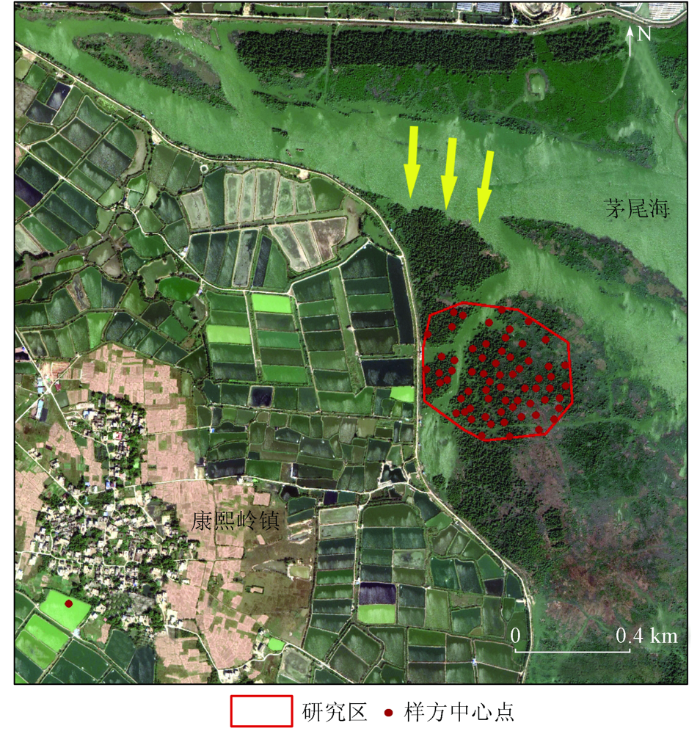
2021年1月在康熙岭红树林保护区共布设了66个10 m×10 m的正方形样方,样方中心点分布位置如图1所示,图中采用地理坐标系GCS_WGS_1984,投影坐标系Albers。在布设样方前确定红树林种类、种植模式和当地潮位信息。记录的信息包括样方中的胸径(在高度1.3 m处量测)、树高以及地理坐标(经纬度)等数量特征。

本次采样,量测1.3 m处树高使用钢卷尺量测,量测胸径使用皮尺量测,如图2所示。以样方为统计单位,结合实地量测到的树高和胸径数据,采用断面积加权法算出无瓣海桑的林分平均树高[15],其具体计算公式为:

H=∑i=1nhigi∑i=1ngi

式中: H为林分平均高; gi为第i棵林木的胸高断面积; hi为第i棵林木的树高; n为样方内所有林木的棵数。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   研究区野外实测样地数据获取

Fig.2   Field measured sample site data acquisition in the study area


2.1.2 机载LiDAR数据获取

2021年1月19日下午3点采用DJI M600 PRO无人机所搭载的普通数码相机和HS40P激光传感器在广西茅尾海康熙岭片区进行红树林飞行试验,从而获得了LiDAR点云数据。当天拍摄的垂直高度约为70 m,航向及旁向重叠度为80%且风力小于2级。本文利用Intertial Explorer(GPS-IMU)后处理软件结合惯性测量单元(inertial measurement unit,IMU)数据以及全球导航卫星系统(global navigation satellite system,GNSS)技术对原始的红树林回波信息进行解算,可以得到研究区的三维激光点云信息(图3)。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   样方机载LiDAR数据

Fig.3   Airborne LiDAR data at the sample site


2.2 研究方法

2.2.1 LiDAR点云树高信息提取

机载LiDAR系统由激光测距装置、成像装置、IMU姿态测量装置和全球定位系统(global positioning system,GPS)接收机4部分组成。它利用GPS和IMU分别可以获得激光源的坐标及激光脉冲的方位。激光测距的原理是测量地表采样点的激光回波脉冲对于发射主波的时间差,从而得到传感器到地面采样点的距离[16]。其测距基本原理可表示为:

D=cT2

式中: D为传感器到目标物体的距离; c为光速; T为激光脉冲从激光器到被测物体的来回传输时间。

使用邵为真等[17]提出的不规则三角网滤波算法将不同密度的LiDAR点云数据分离出地面点云与非地面点云(植被点云),对所获取到的地面点进行插值可生成数字高程模型(digital elevation model,DEM),进而将植被点云高程减去DEM数据可得到植被点云的归一化值,最后利用归一化植被点云可提取相关点云变量。由于LiDAR点云的第一回波对植被冠层的检测更为敏感,本研究采用植被冠层的第一回波数据用于估算林分参数[9](表1),包括百分位数高度15个(hp01,hp05,…,hp95,hp99)、百分位数强度15个(ip01,ip05,…,ip95,ip99)、最大高度\强度(hmax\imax)、最小高度\强度(hmin\imin)、平均高度\强度(hmean\imean)、点云高度\强度标准差(hstddev\istddev)、高度\强度变异系数(hcv\icv)、高度\强度众数(hmode\imode)以及百分位数高度\强度四分位数间距(hiq\iiq)。标准差一般反映用于样方内植被点云高度\强度的离散程度,标准差越大,样方内植被点云高程\强度离散程度越大,反之越小。

表1   用于林分平均高估测的点云特征统计量

Tab.1  Point cloud characteristic statistics for stand mean height estimation

变量变量意义①
hp01\ip01,…,hp99\ip99所有点云1%,…,99%分位数处对应的高度\强度值
hmax\imax样方点云高度\强度的最大值
hmin\imin样方点云高度\强度的最小值
hmean\imean样方点云高度\强度的平均值mean,计算公式为: mean=∑j=1mxjm
hstddev\istddev样方点云高度\强度的标准差stddev,计算公式为: stddev=1m∑j=1m(xj-x-)2
hcv\icv样方点云高度\强度的变异系数cv,计算公式为: cv=stddevmean
imode\imode样方点云高度\强度的众数
hiq\iiq样方点云百分位数高度\强度的四分位数间距iq,计算公式为: iq=p75-p25

①m为每个样方对应归一化植被点云的个数; j为每个样方对应第j个归一化植被点云; xj 为第j植被点云对应的高度值; x¯为植被点云高度均值; p75为样方内点云高度的上四分位数; p25 为样方内点云高度的下四分位数。

新窗口打开| 下载CSV


2.2.2 林分平均高模型的构建

随机森林算法是分类和回归问题中最受欢迎的机器学习算法之一[18]。随机森林模型由多元回归树组成,在构建每棵回归树的过程中,每棵树节点选择分割变量时,先从所有特征变量中随机选取k个特征变量,然后从中找到最优分割点并生成多个回归树模型。每棵回归树的最终预测结果是节点的平均值,随机森林的最终预测结果是所有回归树预测结果的平均值。随机森林算法使用boot-strap采样和bagging集成树算法,并从弱学习者集合中获得最准确的决策。在学习过程中,大约70%的样本(袋内)用于训练阶段,30%的样本(袋外)用于测试阶段。与其他基于树和增强的机器学习型类似,随机森林模型可以模拟每个变量的重要性程度。随机森林模型中最主要的超参数包括最大深度、最小样本叶数、最小样本分裂数、最大特征数和可调树数。ntree表示随机森林所包含的决策树数目,mtry表示每次迭代的变量抽样数值,为了保证预测结果的准确性和计算结果的精度,本文采用ntree=1 000,mtry的取值范围为1~M,其中M为模型构建所涉及的输入变量的总数。

支持向量机作为著名的机器学习方法,常应用于各种非线性问题的求解[19]。它的学习原理是使用一个称为超平面的边界将数据划分为具有近似值的组。 通过分析输入变量与输出变量之间的定量关系,随后建立模型对新观测到的变量进行预测[20]。对于一个分类或回归问题,支持向量机算法用支持向量定义超平面。与其他机器学习模型相比,支持向量机模型包含较少的核函数超参数(线性、多项式或径向基)和正则化参数C,支持向量机模型能够处理非线性数据; 但是,当组成数据较为嘈杂或重叠时,支持向量机模型效率不高。支持向量机模型的性能受核函数选择的影响。为了减少偏差,本文在建模时尝试了5个可能的C,分别为: 0.01,0.1,1,10和100。

同时,还应用人工神经网络的方法建立树高模型。它的原理是先初始化神经网络,给各个权值赋予一个范围在[-1,1]之间的随机数,并将样本数据通过神经网络进行正向传播,同时用均方差计算输出误差。通过逆向传播来不断调节输入层、隐含层和输出层间的权重。当神经网络误差的平方和达到最小值时就结束该算法的计算。神经网络算法不需要对数据的基本关系进行假设,但当计算量大时,训练慢,容易过拟合。由于是“黑箱”,它主要用于预测。decay表示权重衰减,为了平衡计算开销和模型性能,本文在建模时尝试了5个可能的decay,分别为: 0,0.0001,0.001,0.01和0.1[20]。BP神经网络原理如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   BP神经网络原理图

Fig.4   schematic diagram of BP neural network


2.2.3 评估标准

对于林分平均高模型的选择,利用4类指标来评估模型的性能,决定系数R2和均方根误差(root mean square error,RMSE)是衡量回归模型统计误差的标准。较高的R2和较低的RMSE表明机器学习模型的性能更好。此外,本研究还使用了赤池信息准则(Akaike information criterion,AIC)[21]和贝叶斯信息准则(Bayesian information criterion,BIC)[22]来检验所选模型之间的统计差异。AIC和BIC越低,模型的性能越好[23]。计算公式分别为:

R2=1-∑i=1N(yi-y∧i)2∑i=1N(yi-y-)2
RMSE=1N∑i=0N-1(yi-y∧i)2
AIC=Lln(RSSL)+2K
BIC=Lln(RSSL)+Kln(L)

式中: yi为真实值;y∧i为预测值;y-为真实值的平均数; N为验证样品的总数; RSS为残差平方和; K为参数数量(包括截距); L为观测数目。

3 结果与分析

3.1 实测数据特征统计

表2列出了 66个无瓣海桑红树林样方的调查结果。由表2可知,林分平均高的变化范围为3.47~12.02 m,平均值为8.19 m。红树林树高为1.55~13.58 m,胸径为0.70~41.00 cm。红树林实测树高的平均值相比林分平均高的平均值低了0.1 m(表2)。

表2   外业测量树高、胸径和林分平均高的基本统计量

Tab.2  Basic statistics for field measurements of tree height, diameter at breast height, and stand mean height

参数最大值最小值平均值标准差
树高/m13.581.558.092.69
胸径/cm41.000.7015.385.55
林分平均高/m12.023.478.192.28

新窗口打开| 下载CSV


3.2 特征选择

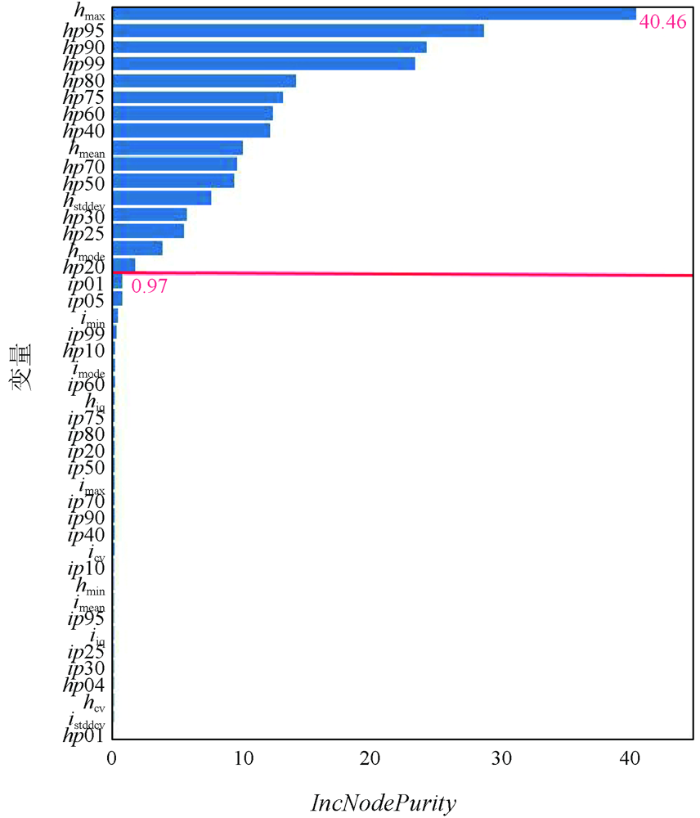
本文对参与红树林树高建模的LiDAR特征变量的重要性进行排序,选择节点不纯度(increase in node purity,IncNodePurity)作为判断LiDAR 特征变量参数重要性的指标。通过比较点云特征统计变量的重要性,特征统计变量的值越大,则特征统计变量的重要性越高(图5)。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   变量重要性图

Fig.5   Variable importance chart


图5中重要性值越高,该特征统计变量对林分平均高估测越重要。从图5中可以看出,利用随机森林算法选择的44个特征变量中,高度统计变量参数hmax对无瓣海桑的林分平均高反演贡献率最大,其次是LiDAR 特征变量中的百分位数高度(hp95,hp90,hp99等),LiDAR点云数据中提取到的强度参数对林分平均高反演贡献较小(红色线为分割线,分割线以上的变量对红树林林分平均高的贡献率较大,分割线以下贡献率较小)。75%~99%分位数高度在研究区无瓣海桑的林分平均高估算中发挥了主要作用,这一发现与前人的研究论断契合[8-9],他们的研究认为: 植被冠层的第一回波的75%~95%分位数高度或最大树高hmax能很好地估测平均树高。本文使用16个贡献率相对较大的特征变量参与随机森林模型的构建,随机森林模型取得了令人满意的结果,训练集和测试集的R2分别为0.985 7和0.938 1,RMSE为0.58 m(表3)。

表3   3种ML模型在林分平均高检索中的性能比较

Tab.3  Comparison of the performance of three ML models in stand mean high retrieval

模型训练集测试集
R2RMSE/mAICBICR2RMSE/mAICBIC
随机森林0.985 70.2836.5921.420.938 10.5880.5049.05
支持向量机0.985 60.3037.1822.000.766 51.2787.8556.40
神经网络0.978 50.3447.0131.840.436 42.90107.6176.16

新窗口打开| 下载CSV


3.3 模型精度对比

将16个贡献率较大的特征变量带入到支持向量机、随机森林和神经网络算法模型中,本研究将70%的样本用于模型的训练,30%的样本用于模型的测试和检验,图6为不同机器学习算法在训练阶段和测试阶段所计算的精度。无瓣海桑林分平均高模型估算的R2越高,RMSE越低,AIC和BIC越低,预测性能越好。由图6可知,支持向量机算法在无瓣海桑林分平均高估算中显示出可接受的结果,测试集中R2为0.766 5,RMSE为1.27 m,AIC为87.85,BIC为56.40; 而神经网络模型的结果相对较差,在测试集中R2值仅为0.436 4。随机森林模型的估算结果在训练集和测试集阶段均表现出较好的结果,R2均达到了0.93以上,总体而言,随机森林模型在研究区域的红树林林分平均高估算中表现最佳。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   不同回归模型的训练和测试结果

Fig.6   Training and testing results of different regression models


3.4 林分平均高的空间分布

由于随机森林模型产生了最佳的预测性能,并且优于其余的机器学习算法,因此本研究选择了随机森林算法模型对研究区无瓣海桑林分平均高进行预测。无瓣海桑林分平均高最终结果被计算成栅格数据,以Tiff格式进行存储。由地理信息系统(geographic information system,GIS)的分类工具将林分平均高数据划分为5类,由图7可知,无瓣海桑林分平均高的模拟结果介于3.90~11.58 m之间。 其中树高超过10 m的无瓣海桑主要分布在研究区潮沟附近及研究区中部,这可能与潮沟水文过程有关,潮沟所带有的营养物质可能给红树林的生长提供了充足的养分。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   林分平均高分布

Fig.7   Mean stand height distribution


4 讨论

本文实测得到北部湾茅尾海(康熙岭片区)的无瓣海桑树高平均值为8.09 m,比张晓君等[24]在广东省珠海市鹤洲北湿地地区统计到的无瓣海桑树高平均值高了0.59 m,也比黄晓敏等[25]在福建省厦门市集美海湾调查得到的无瓣海桑平均树高值高了0.39 m。但是,吴瑞等[26]在海南省东寨港的三江地段得到的无瓣海桑平均树高为14.2 m,高于本研究区的无瓣海桑树高。无瓣海桑的树高不仅与它的生长年龄相关,同时与它生长环境的海水温度、海水盐度、土壤及沉积物、潮汐浸淹频率和海浪能量等因素更是息息相关[27]。低温、生长环境的盐分含量过高或过低均会限制无瓣海桑的生长,并且,不同的红树林植物对潮汐浸淹频率都有相应的适应性,无瓣海桑主要分布在大潮中潮位; 海浪能量太大时,会阻碍无瓣海桑的根系生长[28]。除此之外,无瓣海桑平均高还与模型的精度有着直接的关系,模型的精度不仅受到模型本身因素的影响,而且受到其他多种外部因素的影响[29]。本研究在进行红树林样方调查时并不是直接测量无瓣海桑的林分平均高,而是根据森林的断面积加权法计算林分平均高,断面积加权法的准确度可能会影响模型的估算效果。

随着机器学习算法的发展,林分平均高的估算有了更多的算法。在林分平均高估算算法中,机器学习算法通常比传统的参数方法获得更好的预测性能。Brice等[30]发现在林分平均高估算中,随机森林算法优于线性回归算法。Pourrahmati等[31]研究发现: 在洛里高度(代表了非均匀年龄林分的平均高度)估测中随机森林优于人工神经网络。每种机器学习算法都有自己的适用性和优势,但机器学习方法的选择、参数的确定均对预测模型的精度有一定的影响[32]。因此,本研究采用R语言的“Random Forest”软件包提供的importance进行重要性排序。根据评价指标来获取各模型的最佳参数,利用最佳的参数进行模型模拟。由3种机器学习算法的模拟结果可知,随机森林模型表现出很高的模型拟合能力,其R2在测试集和训练集上均达到了0.938 1以上,RMSE均为0.58 m以下,支持向量机模型次之,该模型在测试阶段的R2为0.766 5,RMSE为1.27 m,神经网络回归模型的拟合效果最差。这些研究结果表明,在对不同的树种选择不同的特征参数时,机器学习算法均表现出一定的差异性。随机森林模型具有变量选择功能,对无信息的预测变量之间的共线性不敏感。然而,支持向量机和神经网络模型往往受到无信息和高度相关预测变量的影响,降低了模型的性能[18]。总之,在本研究区,随机森林算法明显优于其他2种算法,该算法可在北部湾其他地区的红树林林分平均高估算中发挥重要的作用,但是模型最优参数的选择具有一定的不确定性,应该根据实际需要进行参数和变量的优选[11]。

由于受样方环境的影响,样方的选择受到了限制,无法遍及更大的区域。即使模型得到了较为满意的反演结果,但是推广到更大的区域或许精度会受到一定的影响,因此对样方的采集可以选择在退潮时量测更多的红树林数据。未来的研究可能利用机载LiDAR,在更大尺度上对不同沿海地区的无瓣海桑树种进行预测,从而提升随机森林算法在预测红树林林分平均高上的实用性,并寻求一种能获取潮位相对较高区域的实测数据的方法,使得研究范围更大。由于机载LiDAR数据采集成本高,试验仅在典型的小区域进行,未来可以选择尺度上推算法,将LiDAR点云测量的样方数据推演到哨兵数据尺度或者Landsat卫星尺度上。本研究中采用随机森林算法对无瓣海桑的林分平均高进行估算是否适用于其他地区的无瓣海桑或其他红树林树种,尚需进一步检验。

5 结论

本研究以北部湾茅尾海红树林湿地为研究对象,基于机载LiDAR数据采用3种机器学习算法对研究区无瓣海桑的林分平均高进行建模,并反演了研究区的红树林树高空间分布。其主要研究结论如下:

1)研究区林分树高范围为3.47~12.02 m,平均值为8.19 m。

2)样方点云高度最大值hmax对无瓣海桑的林分平均高的贡献率最大,其次是75%~99%分位数高度。

3)随机森林回归模型的预测性能最好(R2=0.938 1,RMSE=0.58,AIC=80.50,BIC=49.05),其次是支持向量机回归模型(R2=0.766 5,RMSE=1.27,AIC=87.85,BIC=56.40),BP神经网络的模型预测性能最差(R2=0.436 4,RMSE=2.90,AIC=107.61,BIC=76.16)。

4)随机森林反演结果可知,树高较高、胸径较大的单木红树林主要分布在研究区潮沟附近以及研究区中部。

参考文献

庞勇, 李增元, 陈尔学, 等.

激光雷达技术及其在林业上的应用

[J]. 林业科学, 2005(3):129-136.

[本文引用: 1]

Pang Y, Li Z Y, Chen E X, et al.

LiDAR remote sensing technology and its application in forestry

[J]. Scientia Silvae Sinicae, 2005(3):129-136.

[本文引用: 1]

Næsset E, Økland T.

Estimating tree height and tree crown properties using airborne scanning laser in a boreal nature reserve

[J]. Remote Sensing of Environment, 2002, 79(1):105-115.

DOI:10.1016/S0034-4257(01)00243-7      URL     [本文引用: 1]

Andersen H E, Mcgaughey R J, Reutebuch S E.

Estimating forest canopy fuel parameters using LiDAR data

[J]. Remote Sensing of Environment, 2005, 94(4):441-449.

DOI:10.1016/j.rse.2004.10.013      URL     [本文引用: 1]

焦义涛, 邢艳秋, 霍达, 等.

基于机载LiDAR点云估测林分的平均树高

[J]. 西北林学院学报, 2015, 30(3):170-174.

[本文引用: 1]

Jiao Y T, Xing Y Q, Huo D, et al.

Study on mean canopy height estimation from airborne LiDAR point cloud date

[J]. Journal of Northwest Forestry University, 2015, 30(3):170-174.

[本文引用: 1]

洪奕丰, 张守攻, 陈伟, 等.

基于机载激光雷达的落叶松组分生物量反演

[J]. 林业科学研究, 2019, 32(5):83-90.

[本文引用: 1]

Hong Y F, Zhang S G, Chen W, et al.

Inversion of biomass components for Larix olgensis plantation using airborne LiDAR

[J]. Forest Research, 2019, 32(5):83-90.

[本文引用: 1]

Li M, Im J, Quackenbush L J, et al.

Forest biomass and carbon stock quantification using airborne LiDAR data:A case study over Huntington Wildlife Forest in the Adirondack Park

[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 7(7):3143-3156.

DOI:10.1109/JSTARS.2014.2304642      URL     [本文引用: 1]

Monnet J M, Chanussot J, Berger F.

Support vector regression for the estimation of forest stand parameters using airborne laser scanning

[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(3):580-584.

DOI:10.1109/LGRS.2010.2094179      URL     [本文引用: 1]

鲁林, 周小成, 余治忠, 等.

随机森林算法在机载LiDAR数据林分平均树高估算中的应用研究

[J]. 地球信息科学学报, 2016, 18(8):1133-1140.

DOI:10.3724/SP.J.1047.2016.01133      [本文引用: 2]

采用机载LiDAR数据估算森林结构参数是当前林业遥感中的研究热点。本文以福建省长汀县朱溪河流域为示范区,探讨了随机森林算法（RF）在机载LiDAR数据林分平均树高估测中的适用性。首先,通过渐进三角网（TIN）算法进行点云滤波并获取相应林分样地的植被点云子集和高程归一化的植被点云;然后,从归一化后的植被点云提取出高度分位数变量以及点云统计特征值等24个变量参数;最后,根据提取的变量参数和野外实测林分均高数据建立研究区林分平均高随机森林回归估测模型。研究结果表明,模型估测的样地平均树高与实测值具有明显线性相关关系,线性回归系数为0.938,相关系数达到0.968。对样地的估测精度都在86%以上,总体平均精度达到了93.17%。研究认为,基于植被点云变量参数的随机森林模型估测林分平均树高具有较高的可靠性。

Lu L, Zhou X C, Yu Z Z, et al.

Plot-level forest height inversion using airborne LiDAR data based on the random forest

[J]. Journal of Geo-Information Science, 2016, 18(8):1133-1140.

[本文引用: 2]

赵勋, 岳彩荣, 李春干, 等.

基于机载LiDAR数据估测林分平均高

[J]. 林业科学研究, 2020, 33(4):59-66.

[本文引用: 3]

Zhao X, Yue C R, Li C G, et al.

Estimation of forest stand mean height based on airborne LiDAR point cloud data

[J]. Forest Research, 2020, 33(4):59-66.

[本文引用: 3]

王德智. 结合UAV-LiDAR和卫星遥感数据的红树林多尺度观测方法研究[D]. 武汉: 中国地质大学(武汉), 2020.

[本文引用: 1]

Wang D Z. Integration of UAV-LiDAR data and satellite imagery for multi-scale mangrove observation[D]. Wuhan: China University of Geosciences(Wuhan), 2020.

[本文引用: 1]

Tian Y C, Huang H, Zhang G Q, et al.

Aboveground mangrove biomass estimation in Beibu Gulf using machine learning and UAV remote sensing

[J]. Science of the Total Environment, 2021, 781:146816-146834.

DOI:10.1016/j.scitotenv.2021.146816      URL     [本文引用: 2]

廖宝文, 郑松发, 陈玉军, 等.

外来红树植物无瓣海桑生物学特性与生态环境适应性分析

[J]. 生态学杂志, 2004(1):10-15.

[本文引用: 1]

Liao B W, Zheng S F, Chen Y J, et al.

Biological characteristics and ecological adaptability for non-indigenous mangrove species Sonneratia apetala

[J]. Chinese Journal of Ecology, 2004(1):10-15.

[本文引用: 1]

邓必玉.

广西钦州沿海无瓣海桑入侵性初探

[J]. 湖北林业科技, 2020, 49(5):46-52.

[本文引用: 1]

Deng B Y.

A preliminary exploration on the eological invasion of Sonneratia apetala in Qinzhou area of Guangxi

[J]. Hubei Forestry Science and Technology, 2020, 49(5):46-52.

[本文引用: 1]

田义超, 黄远林, 张强, 等.

北部湾典型海岛生态系统服务价值空间异质性对比研究

[J]. 海洋科学, 2019, 43(2):60-68.

[本文引用: 1]

Tian Y C, Huang Y L Zhang Q, et al.

A comparative study of spatial heterogeneity of ecosystem service value in typical islands in Beibu Gulf

[J]. Marine Sciences, 2019, 43(2):60-68.

[本文引用: 1]

周生祥.

林分平均树高的求算与分析

[J]. 华东森林经理, 1989(3):37-45.

[本文引用: 1]

Zhou S X.

Calculation and analysis of mean height of tree stand

[J]. East China Forest Management, 1989(3):37-45.

[本文引用: 1]

Baltsavias E P.

Airborne laser scanning:Basic relations and formulas

[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 1999, 54(2-3):199-214.

DOI:10.1016/S0924-2716(99)00015-5      URL     [本文引用: 1]

邵为真, 赵富燕, 梁周雁.

基于不规则三角网的渐进加密滤波算法研究

[J]. 北京测绘, 2016(6):17-21.

[本文引用: 1]

Shao W Z, Zhao F Y, Liang Z Y.

The research of improved progressive triangulated irregular network densification filtering algorithm

[J]. Beijing Surveying and Mapping, 2016(6):17-21.

[本文引用: 1]

Breiman L.

Random forest

[J]. Machine Learning, 2001, 45:5-32.

DOI:10.1023/A:1010933404324      URL     [本文引用: 2]

Gholami R, Fakhari N.

Support vector machine:Principles,parameters,and applications

[J]. Handbook of Neural Computation, 2017, 27:515-535.

[本文引用: 1]

欧强新. 基于机器学习的吉林天然针阔混交林生长建模[D]. 北京: 中国林业科学研究院, 2019.

[本文引用: 2]

Ou Q X. Modeling stand growth of natural conifer and broadleaf mixed forests in Jilin Province based on machine learning[D]. Beijing: Chinese Academy of Forestry, 2019.

[本文引用: 2]

Akaike H T.

A new look at the statistical model identification

[J]. IEEE Transactions on Automatic Control, 1974, 19(6):716-723.

DOI:10.1109/TAC.1974.1100705      URL     [本文引用: 1]

Schwarz G E.

Estimating the dimension of a model

[J]. The Annals of Statistics, 1978, 6(2):461-464.

[本文引用: 1]

Vrieze, Scott I.

Model selection and psychological theory:A discussion of the differences between the Akaike information criterion (AIC) and the Bayesian information criterion (BIC)

[J]. Psychological methods, 2012, 17(2):228-243.

DOI:10.1037/a0027127      PMID:22309957      [本文引用: 1]

This article reviews the Akaike information criterion (AIC) and the Bayesian information criterion (BIC) in model selection and the appraisal of psychological theory. The focus is on latent variable models, given their growing use in theory testing and construction. Theoretical statistical results in regression are discussed, and more important issues are illustrated with novel simulations involving latent variable models including factor analysis, latent profile analysis, and factor mixture models. Asymptotically, the BIC is consistent, in that it will select the true model if, among other assumptions, the true model is among the candidate models considered. The AIC is not consistent under these circumstances. When the true model is not in the candidate model set the AIC is efficient, in that it will asymptotically choose whichever model minimizes the mean squared error of prediction/estimation. The BIC is not efficient under these circumstances. Unlike the BIC, the AIC also has a minimax property, in that it can minimize the maximum possible risk in finite sample sizes. In sum, the AIC and BIC have quite different properties that require different assumptions, and applied researchers and methodologists alike will benefit from improved understanding of the asymptotic and finite-sample behavior of these criteria. The ultimate decision to use the AIC or BIC depends on many factors, including the loss function employed, the study's methodological design, the substantive research question, and the notion of a true model and its applicability to the study at hand.(c) 2012 APA, all rights reserved

张晓君, 管伟, 廖宝文, 等.

珠海人工红树林与天然红树林群落特征比较研究

[J]. 生态科学, 2014, 33(2):321-326.

[本文引用: 1]

Zhang X J, Guan W, Liao B W, et al.

Comparison on the community characteristics between artificial and natural mangroves in Zhuhai City

[J]. Ecological Science, 2014, 33(2):321-326.

[本文引用: 1]

黄晓敏, 卢昌义.

厦门海湾典型无瓣海桑人工种群特征和幼苗更新扩散现状研究

[J]. 生态科学, 2018, 37(5):1-6.

[本文引用: 1]

Huang X M, Lu C Y.

Studies on the characteristics of artificial population of Sonneratia apetala and the current recruitment and dispersal of the seedlings in Xiamen Bay

[J]. Ecological Science, 2018, 37(5):1-6.

[本文引用: 1]

吴瑞, 陈丹丹, 王道儒, 等.

海南省东寨港红树林资源现状调查分析

[J]. 热带农业科学, 2016, 36(9):62-71.

[本文引用: 1]

Wu R, Chen D D, Wang D R, et al.

Survey of mangrove resources in Dongzhai Harbour of Hainan Province

[J]. Chinese Journal of Tropical Agriculture, 2016, 36(9):62-71.

[本文引用: 1]

郑俊鸣, 舒志君, 方笑, 等.

红树林造林修复技术探讨

[J]. 防护林科技, 2016(1):99-103.

[本文引用: 1]

Zheng J M, Shu Z J, Fang X, et al.

Discussion on techniques of mangrove afforestation and rehabilitation

[J]. Protection Forest Science and Technology, 2016(1):99-103.

[本文引用: 1]

廖宝文. 中国红树林恢复与重建技术[M]. 北京: 科学出版社, 2010:20-44.

[本文引用: 1]

Liao B W. Restoration and teconstruction techniques of mangrove forests in China[M]. Beijing: Science Press, 2010:20-44.

[本文引用: 1]

Lu D S, Chen Q, Wang G X, et al.

Aboveground forest biomass estimation with Landsat and LiDAR data and uncertainty analysis of the estimates

[J]. International Journal of Forestry Research, 2012(2):436537-436553.

[本文引用: 1]

Brice M, Michael A W, Geordie W H, et al.

Forest inventory stand height estimates from very high spatial resolution satellite imagery calibrated with LiDAR plots

[J]. International Journal of Remote Sensing, 2013, 34(12):4406-4424.

DOI:10.1080/01431161.2013.779041      URL     [本文引用: 1]

Pourrahmati M R, Baghdadi N, Darvishsefat A A, et al.

Mapping Lorey’s height over Hyrcanian forests of Iran using synergy of ICESat/GLAS and optical images

[J]. European Journal of Remote Sensing, 2018, 51(1):100-115.

DOI:10.1080/22797254.2017.1405717      URL     [本文引用: 1]

Waske B, Benediktsson J A, Árnason, et al.

Mapping of hyperspectral AVIRIS data using machine-learning algorithms

[J]. Canadian Journal of Remote Sensing, 2009, 35(1):106-116.

[本文引用: 1]

/

〈 〉

京ICP备05055290号-2
版权所有 © 2015 《自然资源遥感》编辑部
地址:北京学院路31号中国国土资源航空物探遥感中心 邮编：100083
电话:010-62060291/62060292 E-mail:zrzyyg@163.com
本系统由北京玛格泰克科技发展有限公司设计开发