基于特征空间增强下空谱全变差非负矩阵分解的高光谱解混

doi:10.6046/zrzyyg.2024116

基于特征空间增强下空谱全变差非负矩阵分解的高光谱解混

覃子怡^,, 杨隆珊^,

贵州大学矿业学院,贵阳 550025

Hyperspectral unmixing based on spectral-spatial total variation nonnegative matrix factorization with feature space augmentation

QIN Ziyi^,, YANG Longshan^,

Mining College of Guizhou University, Guiyang 550025, China

通讯作者: 杨隆珊(1992-),女,博士,讲师,主要从事高光谱影像研究。Email:yangls@gzu.edu.cn。

责任编辑: 张仙

收稿日期: 2024-04-1 修回日期: 2024-07-7

基金资助:

国家自然青年科学基金项目“基于深度特征表示模型的稳健高光谐解混方法研究”(43201440)
贵州省科学基金一般项目“联合空谱特征约束下非负矩阵分解方法对高光谱遥感影像的解混研究”(黔科合基础-zk[2022]一般133)
贵州大学博士基金项目“基于特征建模约束非负矩阵分解的高光谱影像解混研究”((2021)67)

Received: 2024-04-1 Revised: 2024-07-7

作者简介 About authors

覃子怡(1999-),女,硕士研究生,主要从事高光谱影像解混研究。Email: qinziyi99@foxmail.com。

摘要

非负矩阵分解(nonnegative matrix factorization,NMF)因其良好的可解释性和易计算性被广泛用于高光谱影像(hyperspectral image,HSI)解混中。为了有效处理HSI中噪声和解混效率问题,该文提出了一种在特征空间增强下的空谱全变差NMF高光谱解混方法(spectral-spatial total variation nonnegative matrix factorization,SSTVNMF)。首先,通过特征提取,将原始数据空间转换到特征空间,在特征空间下进行解混处理,提高解混效率; 其次,为了降低噪声影响,利用双边滤波(bilateral filtering,BF)方法提取空间信息,对特征提取过程进行增强,保证所提取特征的准确性; 最后,为了保证解混方法的性能,基于NMF方法建立顾及空间特征和光谱特征的全变差(total variation,TV)正则化,空间TV通过计算相邻像元之间丰度的水平和垂直差异来促进丰度平滑,光谱TV是基于最小体积TV通过施加端元之间的约束力使体积最小化来增强端元提取。采用美国地质调查局光谱库合成数据作为模拟数据,Jasper Ridge数据集、APEX数据集和Cuprite数据集作为真实数据进行验证,实验结果表明,相比较于其他基于NMF改进的方法,所提方法在定性和定量评价方面都有提高。

关键词： 高光谱解混; 双边滤波; 全变差; 光谱空间信息; 特征提取

Abstract

Nonnegative matrix factorization (NMF) is commonly used in hyperspectral image (HSI) unmixing due to its high interpretability and computability. To effectively address HSI noise and improve unmixing efficiency, this study proposed a method for hyperspectral unmixing based on spectral-spatial total variation nonnegative matrix factorization (SSTVNMF) with feature space augmentation. First, the original data space was converted to the feature space through feature extraction, allowing the unmixing process to be performed in the feature space for enhanced unmixing efficiency. Second, to reduce the impact of noise, the spatial information was extracted using the bilateral filtering (BF) method for enhanced feature extraction, thereby ensuring the accuracy of extracted features. Third, to ensure the effectiveness of the unmixing method, total variation (TV) regularization that considers both spatial and spectral features was established based on the NMF method. The spatial TV promotes abundance smoothing by calculating the horizontal and vertical differences in abundance between neighboring pixels. Based on the minimum-volume TV, the spectral TV enhances endmember extraction by applying constraint forces between endmembers to minimize the volume. Finally, the proposed method was verified using the synthetic data from the USGS spectral library as simulated data and the Jasper Ridge, APEX, and Cuprite datasets as actual data. The experimental results demonstrate that the proposed method outperformed other improved NMF-based methods in terms of qualitative and quantitative assessments.

Keywords： hyperspectral unmixing; bilateral filtering; total variation; spectral-spatial information; feature extraction

PDF (5509KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

覃子怡, 杨隆珊. 基于特征空间增强下空谱全变差非负矩阵分解的高光谱解混[J]. 自然资源遥感, 2025, 37(4): 21-30 doi:10.6046/zrzyyg.2024116

QIN Ziyi, YANG Longshan. Hyperspectral unmixing based on spectral-spatial total variation nonnegative matrix factorization with feature space augmentation[J]. Remote Sensing for Land & Resources, 2025, 37(4): 21-30 doi:10.6046/zrzyyg.2024116

0 引言

随着光谱成像技术的发展,高光谱影像(hyperspectral image,HSI)的光谱分辨率不断提高。高光谱分辨率的成像光谱仪中存在上百个成像波段,每个波段非常窄,成像光谱仪需要大的瞬时视场角来保证较高的信噪比(signal-to-noise ratio,SNR),而高空间分辨率需要较小的瞬时视场角来保证,导致HSI中常常出现混合像元,影响分类处理、地物识别以及其他应用^[1]。高光谱解混被提出来解决混合像元对HSI处理的影响,能够提取混合像元中基本地物的光谱(端元提取)以及计算每个像元中地物的比例(丰度估计)^[2-3]。

非负矩阵分解(nonnegative matrix factorization,NMF)有较好的物理解释性和可计算性,在高光谱解混中得到了广泛研究,但在非凸和不适定问题中很难找到全局最小值^[4]。因此,在NMF中引入约束和正则化项成为提高解混有效性的主要策略之一。HSI的空间信息有助于提高解混精度,例如空间相关性和空间结构等。研究发现,由于HSI中的像元与其邻近的像元通常存在较强的相关性,采用基于稀疏性约束的全变差(total variation,TV)正则化方法可以有效地借助这种空间关联性,使得估计出的端元丰度图更加平滑^[5]。在此基础上通过对HSI数据进行特征提取,能够提取低维特征空间信息,提高计算效率。但HSI在特征提取的过程中,会存在部分特征丢失的问题^[6]。双边滤波(bilateral filtering,BF)通过考虑邻近像元的非线性组合来在保持图像边缘的清晰的同时实现图像的平滑处理,这样能更有效地描绘出图像的空间特性。经过进一步的研究,提出2个步骤的BF操作,第一步用于遥感影像降噪并粗略提取上下文信息,第二步则用于细化影像细节结构^[7]。此外,由于该方法的优越性,可以有效地改善由于TV正则化引起的阶梯效应。

本文以NMF为基础,结合特征提取与空谱全变差(spectral-spatial total variation,SSTV),提出一种在特征空间增强下空谱全变差非负矩阵分解(spectral-spatial total variation nonnegative matrix factorization,SSTVNMF)的高光谱解混方法。首先,引入奇异值分解(singular value decomposition,SVD)方法对原始高光谱数据进行特征提取,将原始高维数据转化为特征矩阵; 同时,为有效抑制影像中噪声影响,将BF与SVD进行结合,提高所提取特征的准确性,从而增强解混模型的性能; 然后,利用TV方法对HSI的空间信息和光谱信息进行提取,充分利用空间邻域光谱信息,构建SSTV约束条件; 最后,在非负矩阵框架下,引入SSTV,对所提取特征进行解混处理,估计出影像中的丰度和端元。

1 线性混合模型

线性混合模型假设端元的数量及其反射光谱是已知的,将高光谱混合模型分解看作是一个线性问题。至今已经提出许多线性混合模型的解决方案,假设在高光谱影像中观察到的像素光谱可以由端元及其相应丰度的线性组合产生,忽略太阳辐射信号在地面不同端元间的多次散射,每一类端元与其对应的丰度之间存在线性关系。方程可表示为:

(1)

y_{i} = \overset{P}{\sum_{j = 1}} a_{i j} s_{j} + n_{i} = A s_{j} + n_{j}

式中: P为端元数; $y_{i}$ 为第i个波段的观测数据; $a_{i j}$ 为端元j在第i个波段上的光谱; $s_{j} = [s_{1 j}, s_{2 j}, \dots, s_{P j}]^{T}$ 为端元对应的丰度向量; $n_{j} \in R^{L}$ 为噪声向量; L为高光谱波段数; $A = [a_{1}, a_{2}, \dots, a_{P}] \in R^{L \times P}$ 为P个端元光谱向量组成的端元矩阵。

将上式写成矩阵形式:

(2)

Y = A S + N s . t . S \geq 0, 1_{P}^{T} S = 1_{K}^{T}

式中: $Y \in R^{L \times K}$ 为观测矩阵; $A \in R^{L \times P}$ 为端元矩阵; $S \in R^{P \times K}$ 为丰度矩阵; $N \in R^{L \times K}$ 为噪声矩阵; K为像素数; $S \geq 0$ 为丰度非负约束; $1_{P}^{T} S = 1_{K}^{T}$ 为丰度和为1的约束, $1_{P}^{T}$ 和 $1_{K}^{T}$ 分别为大小为P和K的列向量。

综上所述,线性混合模型物理意义明确、计算简便且解混精度能够满足实际应用需求,是应用较为广泛的一类模型。

2 特征空间增强的SSTVNMF方法

2.1 BF增强特征提取

SVD在多个领域得到了广泛应用,包括降维^[7]、数据压缩^[8]、去噪^[9]等,该方法能够有效减少高光谱解混中需要考虑的特征数量,同时对于噪声干扰和数据稀疏性问题也提供了解决途径。

任意的矩阵 $Y \in R^{L \times K}$ 都可以通过SVD表示为:

(3)

Y = U Σ V^{T}

式中: $U \in R^{L \times L}$ 为酉矩阵,由L个L维的向量u_l组成,u_l称为左奇异向量; $V \in R^{K \times K}$ 为酉矩阵,由K个K维向量v_k组成,v_k称为右奇异向量; $Σ \in R^{L \times K}$ 矩阵,除主对角线上的元素外,其余元素均为0,主对角线上的元素称为奇异值。

为了提高SVD所提取出特征的可靠性,基于BF原理,利用影像中SNR较高的波段计算权重,将其用于对SNR低的波段进行BF空间滤波处理,以有效抑制高光谱数据中的噪声,此步骤同时考虑了空间信息和光谱信息,在保留边缘的同时,通过水平和垂直像元的非线性组合平滑图像。公式为:

(4)

B F {(Y)}_{p} = \frac{1}{W_{p}} \sum_{q \in r} G_{h} (p - q) G_{d} |I_{p} - I_{q}| I_{q}

(5)

W_{p} = \sum_{q \in r} G_{h} (p - q) G_{d} |I_{p} - I_{q}|

。

式中: r为以像元q为中心的滤波窗口; $I_{p}$ 为滤波窗口内像元p处的灰度值; $G_{h}$ 为空间域标准差δ_h的高斯函数,衡量像元p与q之间的空间距离; $G_{d}$ 为灰度域标准差δ_d的高斯函数,衡量像元p与q之间的亮度或颜色差异; $W_{p}$ 为权重,是空间权重和灰度值权重的乘积。

对高光谱数据进行BF增强,特征提取得到数据如下:

(6)

G = U^{T} (B F (Y) - (\frac{1}{K}) Y)

式中 $G \in R^{(P - 1) \times K}$ 为特征矩阵。

2.2 特征空间增强下SSTVNMF分解

2.2.1 空间TV的NMF分解

HSI中每个像元的光谱信息通常只包含部分端元,所以丰度包含许多0值,具有稀疏性。利用丰度稀疏性对数据进行建模,提高模型表征HSI的能力,从而提高HSI的处理精度。经过特征提取后,HSI维度降为 $G \in R^{(P - 1) \times K}$ ,对特征提取后的特征数据进行解混,稀疏解混问题可以描述为:

(7)

\begin{array}{l} (M, S) = \underset{M, S}{m i n} \frac{1}{2} {(G - M S)}_{2}^{2} + λ {(S)}_{1,1} \\ s . t . S \geq 0, 1_{P}^{T} S = 1_{K}^{T} \end{array}

式中: λ为丰度稀疏约束的参数; $M \in R^{(P - 1) \times P}$ 为特征空间中的端元矩阵。

为了进一步提高NMF算法精度,引入空间TV正则化。空间TV正则化通过考虑像元间的空间相关性,增强模型对空间信息的利用,改善稀疏解混对空间信息利用不足的问题。基于L₁范数的非各向同性全变差正则化,能有效增强有限差分域内丰度矩阵的稀疏特性。引入TV后,可以构建起每个像素的光谱信息与其邻域像素间的联系。这种处理方法不是独立地处理每个像素的值,而是将每个光谱与其邻近光谱的关系纳入考虑,从而更好地利用了空间信息。计算公式为:

(8)

T V (S) = \sum_{(i, j) \in ε} {(s_{i} - s_{j})}_{1}

式中: ε为图像水平和垂直方向上相邻像元集合; s_i和s_j分别对应矩阵S第i和j列向量。

式(8)计算的是相邻像素之间差异的绝对值之和。TV(S)表示非各向同性全变差的扩展形式,其作用是强制丰度相近的相邻像元共享相同的端元,进而促使丰度图实现平滑过渡。通过利用一阶邻域像素之间的相关性,实现了图像解混过程中的空间约束,在空间上的计算表示为 ${(H S)}_{1,1}$ ,H为相邻像元相应丰度之间的水平和垂直差异。因此,HS可以分成2部分:

(9)

[H S] = [\begin{array}{l} H_{h} S \\ H_{v} S \end{array}]

式中: H_h和H_v分别为丰度的水平差异和垂直差异。可以得出,加入空间TV后,式(7)改进为:

(10)

\begin{array}{l} (M, S) = \underset{M, S}{m i n} \frac{1}{2} {(G - M S)}_{2}^{2} + λ {(S)}_{1,1} + λ_{s p a} {(H S)}_{1,1} \\ s . t . S \geq 0, 1_{P}^{T} S = 1_{K}^{T} \end{array}

式中 $λ_{s p a}$ 为空间TV约束的参数。

2.2.2 SSTVNMF

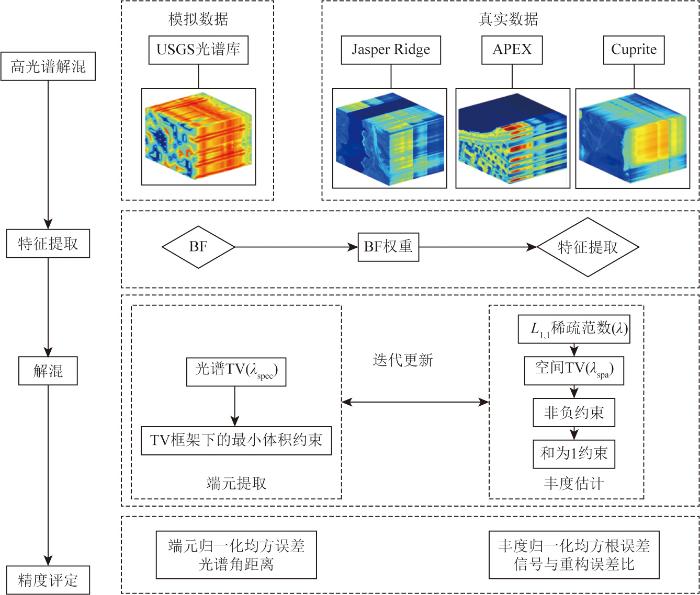
在光谱维度上引入TV正则化,可以在端元间施加一种吸引力,从而强化端元的提取效果^[10]。这样做能够显著地实现体积最小化的特征,优化解混过程中端元的识别与分离。本文在特征空间下将光谱TV正则化引入到空间TV的NMF方法中,形成特征空间增强下的SSTVNMF,算法流程见图1。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 特征空间增强下SSTVNMF的算法流程图

Fig.1 Flow chart of SSTVNMF with feature space

SSTVNMF中光谱TV正则化为:

(11)

R = {(B M - O)}_{2}^{2}

。

式中R为光谱TV正则项重构误差。在TV框架下,B和O为定义正则化的参数,最小体积正则化项由 $B = I_{P} - \frac{1}{P} 1_{P} 1_{P}^{T}$ , $O = 0$ 计算得出。这种方法加强了端元之间的约束力,实现了最小化端元体积。

光谱TV正则化参数控制端元单纯形,即由端元作为顶点的几何凸集。将SSTVNMF相结合,其目标函数表示为:

(12)

\begin{array}{l} (M, S) = \underset{M, S}{m i n} \frac{1}{2} {(G - M S)}_{2}^{2} + λ_{s p e c} {(B M)}_{2}^{2} + \\ λ {(S)}_{1,1} + λ_{s p a} {(H S)}_{1,1} + R_{+} (S) \end{array}

。

式中: $λ_{s p e c}$ 为光谱TV约束的参数; R₊为丰度非负项。

2.3 SSTVNMF优化算法

引入SSTV后,在特征空间下计算出端元矩阵,再利用SVD计算的 $V^{T}$ 恢复端元矩阵A,端元优化公式为:

(13)

A = U \frac{G S^{T}}{2 λ_{s p e c} B B^{T}} + \bar{Y}

。

使用交替方向乘子法(alternating direction method of multipliers,ADMM)优化丰度,这对于求解可分离凸优化问题具有重要意义。主要步骤如下: 对于n个引入变量,首先更新 $S 和 V_{n}$ 作为优化变量,然后依次更新拉格朗日乘子 $D_{n}$ 。具体算法描述如下:

1)引入变量 $V_{1}, V_{2}, V_{3}, V_{4} 和 V_{5}$ 。

2)令 $V_{1} = M S, V_{2} = S, V_{3} = S, V_{4} = H V_{3} 和 V_{5} = S$ 。

3)公式中引入5个拉格朗日乘子D₁,D₂,D₃,D₄和D₅,得到增广拉格朗日方程:

(14)

\begin{array}{l} ￡ (S, V, D) = \frac{1}{2} {(V_{1} - Y)}_{2}^{2} + λ {(V_{2})}_{1,1} + λ_{s p a} {(V_{4})}_{1,1} + R_{+} (V_{5}) + \frac{μ}{2} ({(M S - V_{1} - D_{1})}_{2}^{2} + \\ {(S - V_{2} - D_{2})}_{2}^{2} + {(S - V_{3} - D_{3})}_{2}^{2} + {(H V_{3} - V_{4} - D_{4})}_{2}^{2} + {(S - V_{5} - D_{5})}_{2}^{2}) \end{array}

式中μ为惩罚参数。

4)未知参数部分由式(14)逐项导出,即

(15)

\{\begin{array}{l} S^{k + 1} = \frac{M (V_{1}^{k} + D_{1}^{k}) + V_{2}^{k} + D_{2}^{k} + V_{4}^{k} + D_{4}^{k} + V_{5}^{k} + D_{5}^{k}}{M^{T} M + 3 \times I_{p}} \\ V_{1}^{k + 1} = \frac{Y + μ (M S - D_{1})}{M + μ I_{p}} \\ V_{2}^{k + 1} = s o f t (D_{2} - S, \frac{λ}{μ}) \\ V_{3}^{k + 1} = \frac{D_{3} - S + H (V_{4} + D_{4})}{H^{T} H - I_{p}} \\ V_{4}^{k + 1} = s o f t (D_{4} - H V_{3}, \frac{λ_{s p a}}{μ}) \\ V_{5}^{k + 1} = m a x (D_{5} - S, 0) \end{array}

式中: soft()为非线性软阈值算子; k为迭代次数。

5)最后,更新拉格朗日乘子,即

(16)

\{\begin{array}{l} D_{1}^{k + 1} = D_{1}^{k} + M S - V_{1} \\ D_{2}^{k + 1} = D_{2}^{k} + S - V_{2} \\ D_{3}^{k + 1} = D_{3}^{k} + S - V_{3} \\ D_{4}^{k + 1} = D_{4}^{k} + H V_{3} - V_{4} \\ D_{5}^{k + 1} = D_{5}^{k} + S - V_{5} \end{array}

。

3 结果与分析

为了评估本文方法的有效性,对比了包括本文方法在内的8个方法进行实验,并在模拟和真实数据上评估了各方法性能。本文采用的方法有: SSTVNMF、NMF二次最小体积法(NMF quadratic minimum volume,NMFQMV)^[10]、稀疏增强卷积分解法(sparsity-enhanced convolutional decomposition,SeCoDe)^[11]、图TV正则化 MBO 算法(graph TV regularization merriman-bence-osher,gtvMBO)^[12]、扩展盲端元与丰度提取空间全变分法(extended blind end-member and abundance extraction with total spatial variation,EBEAE-TV)^[13]、保持内在结构不变NMF法(preserve intrinsic structure invariant NMF,PISINMF)^[14]、空间组稀疏正则化NMF法(spatial group sparsity regularized NMF,SGSNMF)^[15]和基于峰度的平滑NMF法(kurtosis-based smooth NMF,KbSNMF)^[16]。其中,SSTVNMF,NMFQMV,PISINMF,SGSNMF和KbSNMF是基于NMF的解混方法,并且SSTVNMF与NMFQMV都采用了TV正则项,前者采用空间光谱TV,后者采用二次光谱TV正则项。SeCoDe,gtvMBO,EBEAE-TV和PISINMF方法是近几年提出的解混方法。通过与相关方法及前沿方法的对比能够更好地验证本文方法的解混效率。

本节的实验分为模拟数据实验和真实数据实验。模拟数据部分分为3个实验,分别是参数设置、噪声鲁棒性分析以及端元数量分析。真实数据部分也分为3个实验: ①展示并比较了每种方法在3个不同真实数据集上的解混性能; ②消融实验分析; ③运行时间分析。

3.1 评价指标

本文采用4个评价指标来评估所提出方法的有效性,包括端元归一化均方误差(normalized mean square error,NMSE)、丰度NMSE、端元光谱角距离(spectral angle distance,SAD)和丰度信号与重构误差比(signal-to-reconstruction error,SRE)。NMSE和SAD的值越小,表示算法精度越高; SRE的值越大表示算法精度越高。评价指标公式分别为:

(17)

N M S E_{A} = \frac{{(\hat{A} - A)}_{F}^{2}}{{(A)}_{F}^{2}}

(18)

N M S E_{S} = \frac{{(\hat{S} - S)}_{F}^{2}}{{(S)}_{F}^{2}}

(19)

S A D = \frac{1}{p} \overset{p}{\sum_{i = 1}} a r c c o s (\frac{A_{i}^{T} {\hat{A}}_{i}}{(A_{i}) ({\hat{A}}_{i})})

(20)

S R E = 10 l g \frac{{(S)}_{F}^{2}}{{(S - \hat{S})}_{F}^{2}}

式中: NMSE_A为端元NMSE; NMSE_S为丰度NMSE; $\hat{A}$ 和 $\hat{S}$ 分别为估计的端元和丰度; $‖ ‖_{F} 为 F 范数$ ; A_i为第i个端元。

3.2 实验数据

模拟数据通过美国地质调查局(united states geological survey,USGS)光谱库生成,该数据库包括近500种标准矿物,反射率值均匀分布在224个光谱波段,波长在400~2 500 nm之间(http://speclab.cr.usgs.gov/spectral.lib06)^[17]。本文采用的模拟数据是选取USGS光谱库中5种矿物的光谱作为端元线性合成的,共有224个波段,单波段图像大小为81像素×81像素。

真实HSI数据集包括 Jasper Ridge数据集^[18]、APEX数据集^[19]和Cuprite数据集^[20]。

1)Jasper Ridge数据集原始图像尺寸为512像素×614像素,共有224个波段,波长范围在380~2 500 nm之间,光谱分辨率为9.46 nm,该数据集的端元分别是水、树、土壤和道路。采用100像素×100像素的子图像进行实验,在去除掉受密集水蒸气和大气效应影响的波段后,保留了198个波段。

2)APEX数据集是通过机载棱镜实验(airborne prism experiment,APEX)^[19]生成的高光谱数据集。本实验使用的APEX数据集共有285个波段,单个波段的图像大小为100像素×100像素,该数据端元分别是道路、树木、屋顶和水^[21]。

3)Cuprite数据集来自位于美国内华达州的Cuprite矿区,获取时间为1997年。原始数据共有224个波段,波长在370~2 480 nm之间,该数据集的端元分别是蒙脱石、沙漠漆和明矾石。采用50像素×90像素子图像进行实验,去除噪声波段与富含水蒸气波段后,保留188个波段。

3.3 模拟实验结果及分析

首先通过模拟数据参数设置实验得到了本文方法的参数最优值,再根据参数最优值进行噪声鲁棒性分析(即SNR∈{5,10,15,20,25,30,35})和端元数量(即P∈{3,4,5,6,7,8})实验。每个实验计算5次结果,统计实验结果的均值和方差,以证明所提出方法解混效率及有效性。

3.3.1 参数分析

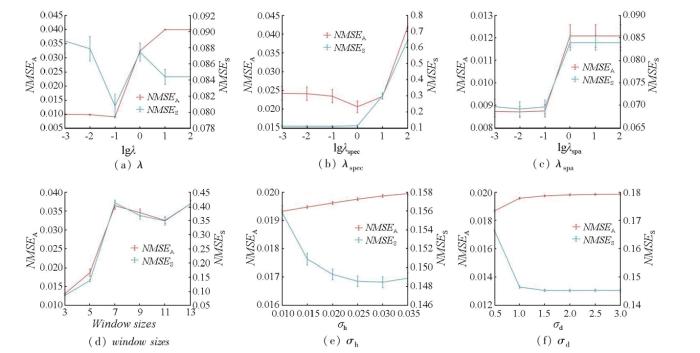
在特征空间增强下的SSTVNMF目标函数中有6个参数,分别是丰度稀疏参数λ、光谱TV参数 $λ_{s p e c}$ 、空间TV参数 $λ_{s p a}$ 、窗口r的尺寸window sizes、空间域标准差 $σ_{h}$ 、灰度值域标准差 $σ_{d}$ 。在实验中,根据经验将预定义的误差容限设置为10^-8,最大迭代次数设置为200次。如图2所示, $σ_{h}$ 和 $σ_{d}$ 对端元具有较强的鲁棒性,对丰度的影响比较大,因此可以根据NMSE_S最小值处来确定 $σ_{h}$ 和 $σ_{d}$ 的最优参数。因此,选择 $λ$ =10^-1, $λ_{s p e c}$ =10¹, $λ_{s p a}$ =10^-1,Window sizes=3, $σ_{h}$ =0.025, $σ_{d}$ =1.5进行后续实验。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 参数对于特征空间增强下的SSTVNMF算法性能的影响

Fig.2 Effect of SSTVNMF in feature space parameters on the unmixing performance

3.3.2 噪声鲁棒性分析

本节实验对特征空间增强下的SSTVNMF方法的抗噪性进行评价,并与其他对比方法(NMFQMV,SeCoDe,gtvMBO,PISINMF,EBEAE-TV,SGSNMF,KbSNMF)进行定量比较。为了进行充分对比,在模拟数据中加入不同SNR的噪声,分析本文方法对噪声的鲁棒性。

首先采用3.3.1中得到的6个最优参数值,然后将SNR分别设置为5 dB,10 dB,15 dB,20 dB和25 dB进行解混效果比较。

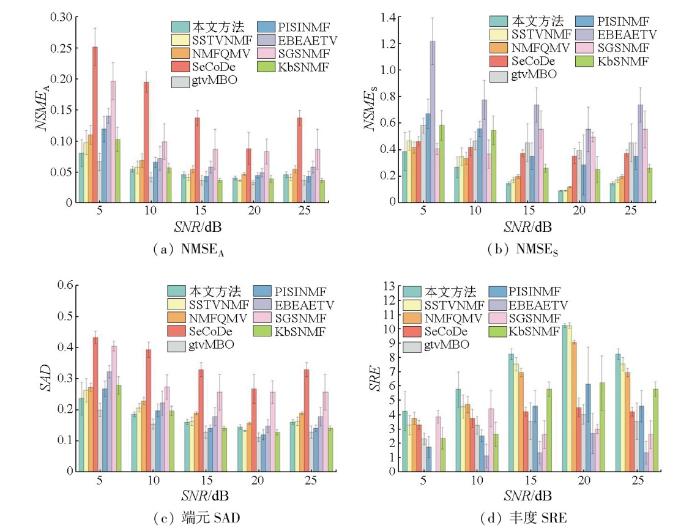
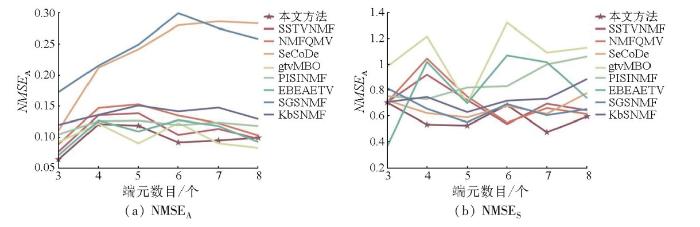
图3展示了不同SNR下NMSE_A,NMSE_S,SAD,SRE的均值和标准差。随着SNR增加,所有方法的NMSE_A,NMSE_S,SAD呈下降趋势,SRE呈上升趋势。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 SNR对算法性能的影响

Fig.3 Effect of SNR on the unmixing performance

实验验证该方法对不同SNR值的鲁棒性。对于不同SNR,特征空间增强下的SSTVNMF方法在NMSE_S和SRE方面取得了最好的效果; 在NMSE_A和SAD方面,特征空间增强下的SSTVNMF方法的性能仅次于gtvMBO方法。相较于SSTVNMF方法,本文提出的考虑BF增强特征空间的SSTVNMF方法在不同SNR下的指标都更好,这是由于引入BF对特征空间进行增强能够有效提取数据特征,降低数据量,减小噪声影响,以此获得更高质量的解混结果。再与NMFQMV方法进行对比,本文提出的方法也展示出更鲁棒的评价指标值,验证SSTV在解混中能够更好地平滑丰度,进而迭代出更准确的端元。因此,在各信噪比下,特征空间增强下的SSTVNMF方法计算出的端元丰度图都更加接近真实端元丰度图。

3.3.3 端元数量分析

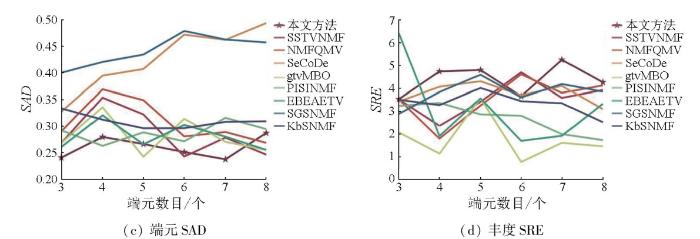
采用不同端元数量的模拟数据对所有方法的性能进行了测试,将模拟数据的SNR固定为20 dB,端元个数设置为3,4,5,6,7,8。结果如图4所示。

图4-1

新窗口打开| 下载原图ZIP| 生成PPT

图4-1 端元数量对算法性能的影响

Fig.4-1 Effect of endmember numbers on the unmixing performance

图4-2

新窗口打开| 下载原图ZIP| 生成PPT

图4-2 端元数量对算法性能的影响

Fig.4-2 Effect of endmember numbers on the unmixing performance

图4结果显示,所有方法的性能都随着端元数量的增加而降低,特征空间增强下的SSTVNMF方法在不同端元数量上的解混能力平均优于其他方法,尤其在端元数量低于5的情况下,本文提出的方法在丰度估计上取得明显优势,也验证了特征提取与TV对丰度噪点平滑的优势。综上,特征空间增强下的SSTVNMF在不同端元情况下优于其他方法,证实了其对不同端元数量的高光谱数据实验具有稳定性。

3.4 真实实验结果及分析

本节采用3个真实数据集进行实验,通过真实数据集上的解混结果和运行时间来验证特征空间增强下的SSTVNMF方法的有效性,并通过空间TV、光谱TV和BF的消融实验来验证3个正则项对解混的影响程度。

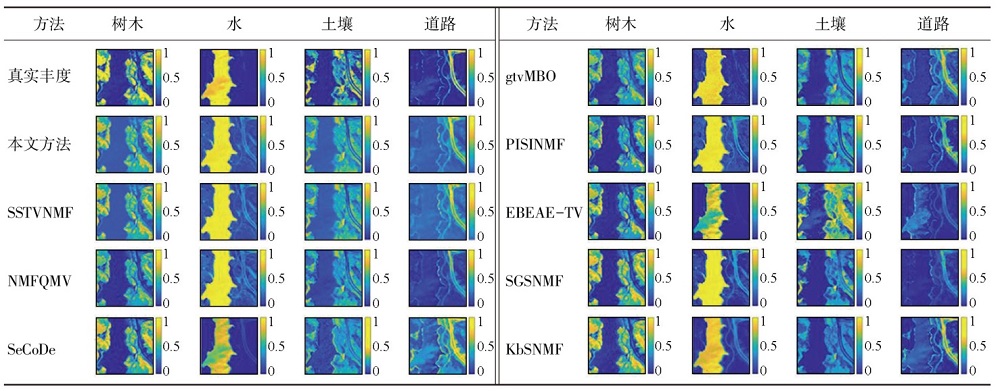
3.4.1 解混结果

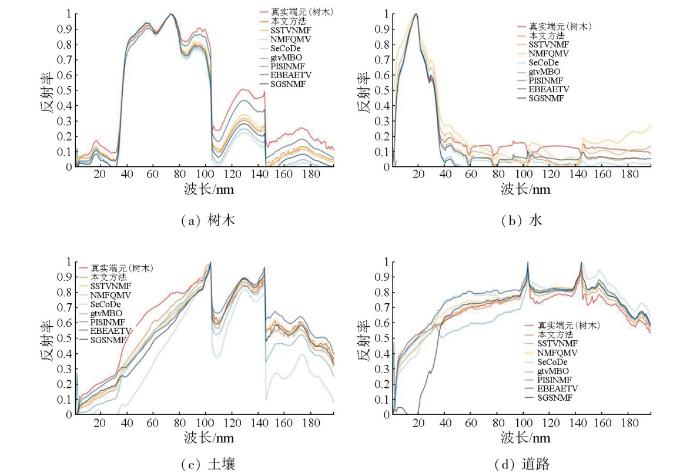
图5和表1分别展示了Jasper Ridge数据集下,不同算法得到的端元和丰度的结果。如图5所示,可以明显看出特征空间增强下的SSTVNMF提取的端元与真实端元较为一致,与真实端元的相似度比其他对比方法高。如表1所示,特征空间增强下的SSTVNMF方法的丰度图与真实丰度相似度高,并且对影像中的噪声进行了平滑处理,在真实的丰度图中,亮部表示相应端元的丰度较高。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 特征空间增强下的SSTVNMF与其他对比方法在Jasper Ridge数据集上的端元提取图

Fig.5 Endmember extraction of SSTVNMF in feature space and other comparison methods on the Jasper Ridge dataset

表1 特征空间增强下的SSTVNMF与其他对比方法在Jasper Ridge数据集上的丰度估计

Tab.1 Abundance estimation of SSTVNMF in feature space and other comparison methods on the Jasper Ridge dataset

新窗口打开| 下载CSV

表2提供了特征空间增强下的SSTVNMF方法与其他方法处理3个不同真实数据集时,实验结果以及运行时间的量化对比情况。为了使定量评价指标展示更加清晰,在真实数据上进行的实验只展示SAD与SRE指标,分别代表端元提取和丰度估计的精度。

表2 特征空间增强下的SSTVNMF与其他对比方法在3个真实数据集上的评价指标和运行时间

Tab.2 Evaluation metrics and running time of SSTVNMF in feature space and other comparison methods on true dataset

算法	Jasper Ridge数据集			APEX数据集			Cuprite数据集
算法	SAD	SRE	运行时间/s	SAD	SRE	运行时间/s	SAD	SRE	运行时间/s
本文方法	0.141 6	10.590 9	0.51	0.138 0	11.762 0	4.23	0.398 4	9.284 1	0.76
SSTVNMF	0.141 9	10.505 2	0.32	0.138 1	11.761 9	3.78	0.391 7	9.177 2	0.50
NMFQMV	0.147 9	8.976 2	1.20	0.138 3	11.963 5	1.08	0.400 0	8.272 6	1.31
SeCoDe	0.215 8	8.420 6	22.78	0.163 5	3.079 8	6.20	0.280 5	7.026 8	13.50
gtvMBO	0.217 9	8.073 6	0.01	0.141 1	-0.274 9	0.01	0.263 7	4.308 5	0.01
PISINMF	0.119 8	9.916 9	2.70	0.147 9	7.380 3	1.53	0.434 3	10.044 9	3.70
EBEAE-TV	0.237 7	11.701 6	2.13	0.129 8	-1.452 3	1.17	0.288 2	4.799 4	3.37
SGSNMF	0.257 7	7.170 6	3.93	0.146 0	3.185 9	0.71	0.274 8	5.097 6	6.56
KbSNMF	0.137 8	9.243 5	6.83	0.139 8	11.132 1	3.05	0.409 2	8.793 3	14.74

新窗口打开| 下载CSV

通过表2给出的数据定量分析,特征空间增强方法对于端元提取的提升较低,原因可能是高光谱数据中的噪声波段对于端元间的区分影响较小,如表2所示,在Japer Ridge和Cuprite数据集实验中,相较于SSTVNMF,本文方法在丰度估计精度方面有明显提升,且Cuprite处于矿区,矿物混合紧密,使得空间信息更加复杂,通过引入特征空间提取可以充分利用HSI中的空间信息,提升解混效果,使得本文方法取得了优秀的丰度估计精度; 但在APEX数据集中,本文方法对端元丰度的提升都比较小,原因在于APEX数据集的噪声较小,导致BF对特征空间增强的效果不明显。综上可知,在噪声大的数据集,SRE值展示出特征空间增强下的SSTVNMF方法的丰度提取效果精度较高,由此可以看出,本文提出的特征空间信息有助于丰度估计。

通过表2给出的9种方法在3个不同的真实数据集上的解混效率,gtvMBO平均耗时短,SeCoDe平均耗时长,由于SeCoDe通过以基于张量的方式联合捕获HSI的空间光谱信息,运算量较大,从而延长了运行时间。在复杂数据上,特征空间增强下的SSTVNMF的计算效率低于SSTVNMF与gtvMBO,但端元提取和丰度估计的精度更高。

3.4.2 消融实验

为验证本文提出的SSTV和BF的有效性,本节对空间TV、光谱TV和BF进行消融实验。为保证实验结果的准确性,统一采用图1中的最优参数进行实验结果对比。结果如表3所示。

表3 在Jasper Ridge数据集的光谱TV、空间TV和双边滤波消融实验 Fig.3 Blation experiments with Jasper Ridge data for TV_spec, TV_spa, and BF

算法	约束项			评价指标
算法	空间TV	光谱TV	BF	SAD	SRE
NMFQMV	√^①	×	×	0.147 9	8.976 2
SSTVNMF	√	√	×	0.141 9	10.505 2
本文方法	√	√	√	0.141 6	10.590 9

①√代表加入该约束项,×代表未加入该约束项。

新窗口打开| 下载CSV

如表3所示,引入单一光谱TV约束的NMFQMV方法的端元提取与丰度估计均为最差的,这在一定程度上说明SSTV分别在丰度和端元方面提高了解混性能。而相较于SSTVNMF方法,特征空间增强下的SSTVNMF方法的端元丰度结果都更好,证明SSTV与BF联合约束的解混精度优于单一TV的方法,进一步证明本文所提出的联合约束对解混是有效的,验证了SSTV与BF处理的重要性。

4 结论

本文针对HSI数据量大、受噪声影响的问题,结合空间光谱信息,提出一种稳健的特征空间增强下的SSTVNMF方法,该方法将SSTV和BF集成到NMF中。并通过模拟和真实数据实验,验证了该方法的有效性,从实验结果可以看出特征空间增强下的SSTVNMF方法得到较好的解混结果。

1)针对HSI复杂性强、数据量大的问题,首先对高光谱数据进行特征提取处理,降低数据量; 引入BF降低原始数据中的噪声波段影响,实现BF增强特征提取。利用BF获取非平稳空间信息,提高了该方法空间特征表示能力的同时降低了噪声影响。

2)针对NMF存在非凸的问题,引入SSTV,以此利用高光谱数据丰富的空间光谱信息,提高方法的鲁棒性。在丰度上引入TV,通过计算相邻像元之间丰度的水平和垂直差异来促进丰度平滑; 对端元引入最小体积约束获取空间和光谱信息,实现SSTV,能够在优化丰度和端元的同时保留图像边缘。

综上所述,本文提出的特征空间增强下的SSTVNMF方法在高光谱解混中具有有效性。不过,在噪声较小的HSI中,BF对特征提取的增强效果并不明显,未来的研究可以从增强低噪声数据特征提取的方向入手。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

苏远超, 许若晴, 高连如,

等.

基于深度学习的高光谱遥感图像混合像元分解研究综述

[J]. 遥感学报, 2024, 28(1):1-19.