基于神经网络的InSAR/GNSS深度融合尾矿库坝体时序监测及预测研究

doi:10.6046/zrzyyg.2024271

基于神经网络的InSAR/GNSS深度融合尾矿库坝体时序监测及预测研究

吕林伟^,¹^,², 王瑞^,¹^,², 许林涛³, 黄诗乔¹, 黄帅帅⁴, 林敏⁵, 贺一波⁶, 何倩⁷, 晏慧能¹^,², 陈尚波⁸

1.赣南科技学院资源与土木工程学院，赣州 341000

2.赣州市资源与环境遥感重点实验室，赣州 341000

3.中国石油集团渤海石油装备制造有限公司，天津 300280

4.江西理工大学土木与测绘工程学院，赣州 341000

5.安徽省龙桥矿业股份有限公司，合肥 230000

6.山西能源学院，晋中 030600

7.湖北国土资源职业学院，武汉 430090

8.江西省应急管理科学研究院，南昌 330000

Time-series monitoring and prediction of tailings dams through neural network-based deep infusion of InSAR and GNSS data

LYU Linwei^,¹^,², WANG Rui^,¹^,², XU Lintao³, HUANG Shiqiao¹, HUANG Shuaishuai⁴, LIN Min⁵, HE Yibo⁶, HE Qian⁷, YAN Huineng¹^,², CHEN Shangbo⁸

1. College of Resources and Civil Engineering，Gannan University of Science and Technology，Ganzhou 341000，China

2. Ganzhou Key Laboratory of Remote Sensing for Resources and Environment，Ganzhou 341000，China

3. CNPC Bohai Oilfield Equipment Manufacturing Co.，Ltd.，Tianjin 300280，China

4. School of Civil and Surveying Engineering，Jiangxi University of Science and Technology，Ganzhou 341000，China

5. Anhui Longqiao Mining Co.，Ltd.，Hefei 230000，China

6. Shanxi Energy Institute，Jinzhong 030600，China

7. Hubei Vocational College of Land and Resources，Wuhan 430090，China

8. Jiangxi Provincial Emergency Management Science Research Institute，Nanchang 330000，China

通讯作者: 王瑞（1985-），男，副教授，主要从事InSAR/GNSS数据处理及应用研究。Email：wangrui@gnust.edu.cn。

责任编辑: 李瑜

收稿日期: 2024-08-16 修回日期: 2025-01-3

基金资助:

国家自然科学基金项目“UAV/InSAR深度融合采动区地表形变损坏信息提取关键技术研究”(52364018)
江西省应急管理科学研究院自主研发计划项目“InSAR技术多因素扰动离子型稀土原地浸矿边坡失稳动态监测研究”(YKY-ZY-2024-01)

Received: 2024-08-16 Revised: 2025-01-3

作者简介 About authors

吕林伟（2003-），男，主要从事尾矿库形变监测研究。Email：719519920@qq.com。

摘要

尾矿库坝体稳定性时序监测及预测一直都是我国矿山产业安全方面研究重点。该文利用InSAR与GNSS技术获取安徽省某尾矿库坝体表面6个特征监测点的26期纵向形变数据，通过建立附有限制参数的平差模型，以监测点的初始三维坐标作为多项式改正参数，对合成孔径雷达干涉测量技术（interferometric synthetic aperture Radar，InSAR）数据与全球导航卫星定位系统（global navigation satellite system，GNSS）数据进行融合以提高数据精度，并利用BP神经网络对监测点的形变数据进行时序预测，从而得到监测点的未来形变数据。实验结果表明，GNSS与InSAR数据融合后以均方根误差（root mean square error，RMSE）作为精度评定标准，计算并比较融合前、后每一期形变数据与形变真值的RMSE，得到融合后RMSE较融合前下降最多70.61%，平均下降25.91%。采用神经网络模型对融合后的1~22期InSAR数据反复训练，以23~26期InSAR形变数据作为测试集，最后输出各点23~26期数据。通过与GNSS数据计算各点网络输出值RMSE<1.5 mm。研究成果能够为尾矿库坝体时序稳定性监测及预测提供可靠技术支撑。

关键词： 尾矿库; SBASInSAR; 附有限制参数的平差模型; BP

Abstract

The time-series monitoring and prediction of tailings dam stability have always been a major concern in China’s mine safety research. Focusing on a tailings dam in Anhui province，this study obtained 26 periods of longitudinal deformation data from six characteristic monitoring points on the dam surface，using InSAR and GNSS technologies. Based on the data，a least-squares adjustment model with restricted parameters was established. Combined with the initial three-dimensional coordinates of the monitoring points as polynomial correction parameters，the InSAR and GNSS data were fused to improve the data accuracy. Then，time-series prediction of deformation data was conducted for the monitoring points using the back propagation （BP） neural network，thus obtaining their future deformation data. Experiments were carried out to compute and compare the deformation data and corresponding root mean square error （RMSE） of each period before and after fusion，wherein the fused GNSS and InSAR data were evaluated with the root mean square error （RMSE） as the accuracy standard. The results showed that the post-fusion RMSE decreased by up to 70.61% and by at least 4.34% （average：25.91%），compared to pre-fusion data. Furthermore，the neural network model was used to repeatedly train the fused InSAR data from periods 1 to 22，with periods 23 to 26 serving as the test set，ultimately outputting the data of each point for periods 23 to 26. Compared to the GNSS data，the RMSE of the outputs were less than 1.5 mm. These results can provide reliable technical support for the time-series monitoring and prediction of tailings dam stability.

Keywords： tailings pond; SBASInSAR; least-squares adjustment model with restricted parameters; back propagation （BP）

PDF (4130KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

吕林伟, 王瑞, 许林涛, 黄诗乔, 黄帅帅, 林敏, 贺一波, 何倩, 晏慧能, 陈尚波. 基于神经网络的InSAR/GNSS深度融合尾矿库坝体时序监测及预测研究[J]. 自然资源遥感, 2025, 37(5): 162-171 doi:10.6046/zrzyyg.2024271

LYU Linwei, WANG Rui, XU Lintao, HUANG Shiqiao, HUANG Shuaishuai, LIN Min, HE Yibo, HE Qian, YAN Huineng, CHEN Shangbo. Time-series monitoring and prediction of tailings dams through neural network-based deep infusion of InSAR and GNSS data[J]. Remote Sensing for Land & Resources, 2025, 37(5): 162-171 doi:10.6046/zrzyyg.2024271

0 引言

尾矿库是每个矿山产业不可缺少的一部分，其通常是采用坝体围堰的方式建筑，主要是用以堆存和管理矿石选别加工后排出的尾矿或其他工业废渣。由于各种尾矿或工业废渣的堆积，尾矿库成为一个具有高势能的人造泥石流危险源，亦是矿山产业中最大的危险源，存在溃坝风险，而矿坝一旦发生崩溃，对于尾矿库下游的居民安全和各种设施会造成严重的威胁。历史上，国内外均发生过严重的大型尾矿库崩溃事件，2008年9月8日，山西省临汾市襄汾县新塔矿业有限公司980沟尾矿库发生溃坝事故，造成277人死亡、4人失踪；2015年1月25日，巴西淡水河谷公司尾矿库发生溃坝事故，造成350多人死亡或失踪^[1]。而最新数据表明，我国共有近8 000座尾矿库，数量居世界第一，所以，对尾矿库坝体表面形变稳定性的监测与预测是一项必不可缺的重要工作。

目前，传统水准测量手段虽然测量精度高，但存在监测效率低、成本大且无法区域形变量等缺陷，在尾矿库的形变监测中已较少使用。而随着近年来合成孔径雷达干涉测量技术（interferometric synthetic aperture Radar，InSAR）与全球导航卫星定位系统（global navigation satellite system，GNSS）的发展，多数学者提出使用GNSS与InSAR对大范围地表形变进行时序监测，马东升^[2]通过建立GNSS在线监测系统对尾矿库进行形变监测，证明GNSS为尾矿库监测带来许多便利；陈娅男^[3]表明时序INSAR技术在尾矿库形变监测上有重大意义。

InSAR技术在形变监测上虽然具备全天候、全天时、成本低、范围广、空间分辨率高等优点^[4]，但由于自身技术限制，其易受大气延迟误差、时空失相干噪声、地面环境变化等影响，导致在时间域的分辨率达不到非常高的要求，测得结果中包含一定粗差。而在线GNSS作为一种精密定位手段，可以较好地消除电离层、对流层误差带来的影响，得到相较于InSAR数据精度更高的数据。尽管GNSS能够连续长期地监测地面情况，在时间域上的分辨率很高，但由于受到GNSS装置与组网形式的限制，其只能进行单个或少量点的精密监测，要想在大面积范围内使用GNSS技术进行监测，需要耗费大量的人力与财力。而这类劣势恰好可与InSAR技术的优势进行互补，于是利用GNSS与InSAR监测技术的自身优点，让两者共同发挥各自优势，成为一项有意义的研究方向。对此，国内众多学者提出INSAR/GNSS数据融合概念，其中，许才军等^[5]提出建立多种模型与算法将GNSS与INSAR数据融合研究展望；刘国林等^[6]对GNSS与INSAR融合可行性进行分析并证实二者融合具有重大的实用价值；曹海坤等^[7]提出利用附加系统误差参数的升降轨InSAR-GPS数据融合方法建立模型对InSAR-GPS数据进行融合并验证其可行性。

目前，常使用的时序预测手段有自回归移动平均模型（autoregressive integrated moving average mo-del，ARIMA）、长短期记忆网络（long short term memory，LSTM）、灰色预测模型、卡尔曼滤波、BP神经网络模型等，而本文通过对王洲^[8]附加系统参数的GNSS/INSAR融合模型进行改进，提出以监测点三维原始曲面坐标作为附加系统参数建立的INSAR/GNSS数据融合模型系统，利用该模型对尾矿库地面形变INSAR数据进行误差改正，并将误差改正后的数据利用BP神经网络预测，以实现对尾矿库表面未来形变数据的预测从而对坝体安全性进行检验。

1 研究区概况及数据源

1.1 研究区概况

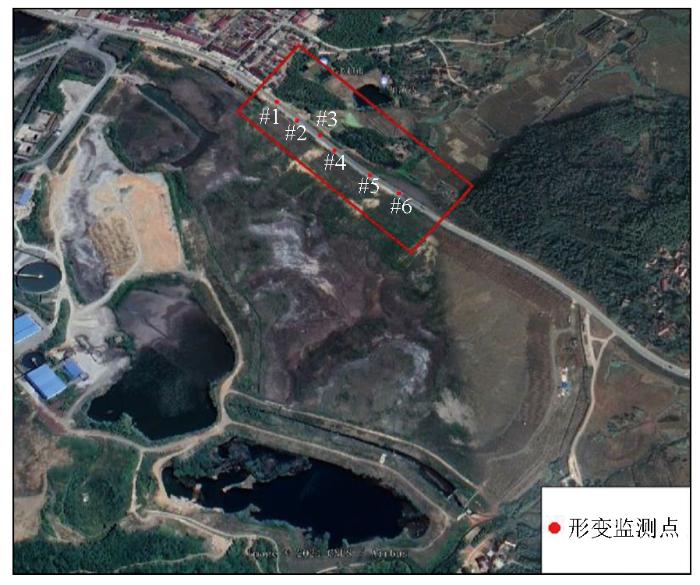
本文研究区域为安徽省某矿业有限公司尾矿库坝体。该公司后家冲尾矿库位于安徽省庐江县黄屯乡龙桥村境内，由山东省黄金集团烟台设计研究工程有限公司设计。尾矿库主要区域及监测点大致位置如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 监测区地理位置及点位大致分布图

Fig.1 Geographic location and approximate distribution map of monitoring area

1.2 数据源

本文选取尾矿库坝体6个形变情况具有显著特征的GNSS点位，获取2023年1—11月间26组数据，分别为GNSS与InSAR相对应的形变数据。由于InSAR数据测得为雷达视线（line of sight，LOS）向形变，利用式（1）将其转化为纵向形变数据^[9]，计算公式为：

（1）ΔH=d_LOS/cosθ ，

式中：ΔH为纵向形变量；θ为雷达入射角；d_LOS为雷达LOS向上形变量。各点位初始三维坐标如表1所示。

表1 观测点三维空间坐标数据

Tab.1 3D spatial coordinate data of observation points

观测点	X	Y	Z
#1	4 695.661	5 138.075	30.438
#2	4 667.625	5 166.371	30.377
#3	4 639.355	5 194.903	30.446
#4	4 611.383	5 223.137	30.502
#5	4 583.200	5 251.577	30.466
#6	4 554.937	5 280.115	30.271

新窗口打开| 下载CSV

2 数据融合及预测模型

2.1 SBAS-InSAR技术监测原理

SBAS-InSAR技术是近年来基于InSAR技术提出的一种新型时序地表形变监测方法，能够很好地改善常规InSAR技术在时空基线失相关的问题，从而提高InSAR精度和时间连续性^[10]。与传统的干涉测量方法相比，该方法能够解决空间不相干和时间不相干的问题。其主要是通过对时空基线设置阈值，将获得的全部合成孔径雷达（synthetic aperture Radar，SAR）影像分成多个组合，得到多个小基线集合，然后对各集合内部利用最小二乘法，集合之间利用奇异值分解法的联合解算来得到高精度的时间序列形变值。

假设在t₁~t_n时间段中获取了M幅同一研究区域的SAR影像，选取其中一幅影像图作为主影像^[11]，根据干涉组合原理，设置组合阈值，形成N幅干涉图，同时满足下式^[12]：

（2）$\frac{M}{2}$≤N≤$\frac{M（M-1）}{2}$，

对于其中t_a和t_b（t_a<t_b）时刻生成的第i（i=1，2，…，N）幅干涉影像，对其进行去除平地效应和地形相位的影响后，第x个像素的干涉相位^[13]模型为：

（3）${\varphi }_{a，b}^{i}$（x，r）=${\varphi }_{def}^{i}$（x，r）+${\varphi }_{topo}^{i}$（x，r）+
${\varphi }_{aps}^{i}$（x，r）+${\varphi }_{orb}^{i}$（x，r）+${\varphi }_{noise}^{i}$（x，r），

式中，${\varphi }_{a，b}^{i}$（x，r）为t_a~t_b对应的LOS向最终形变相位；${\varphi }_{def}^{i}$（x，r）为沿LOS向的形变相位；${\varphi }_{topo}^{i}$（x，r）为地形相位误差；${\varphi }_{aps}^{i}$（x，r）为大气相位误差；${\varphi }_{orb}^{i}$（x，r）为基线轨道引起的相位误差；${\varphi }_{noise}^{i}$（x，r）为噪声误差。

假定不同干涉图间的形变速率为v_k_，_k₊₁，则t_a~t_b之间的累积形变模型为：

（4）ϕ_def（x，r）=$\frac{4\pi }{\lambda }\sum _{k={t}_{a}}^{{t}_{b}-1}$（t_k-t_k₊₁）v_k_，_k₊₁ 。

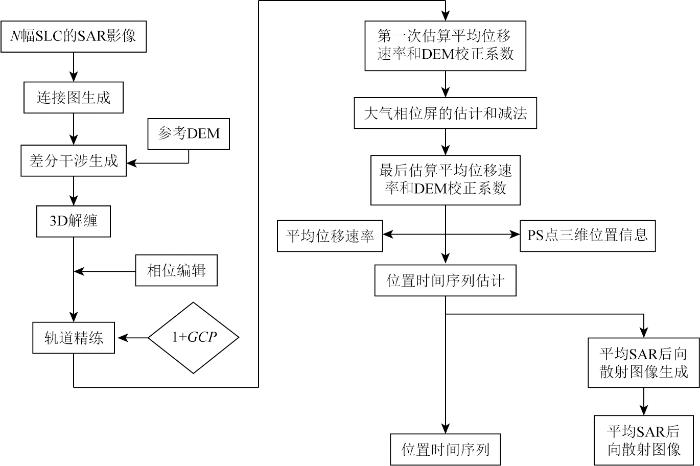
对N幅干涉条纹图进行三维时空相位解缠即可求出不同SAR获取时间的形变速率^[14]。图2为SBAS-InSAR数据主要处理流程。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 InSAR数据处理流程

Fig.2 InSAR data processing flow

2.2 GNSS/InSAR数据融合模型

本实验以现代测量平差模型为基础，以GNSS数据作为真值，通过建立附有限制参数的平差模型建立GNSS/InSAR融合模型，利用模型对InSAR数据进行改正以提高InSAR监测数据的精度，其原理主要如下^[15]：

假设某一时期中某一点i的GNSS与InSAR监测数据分别为${D}_{GNSS}^{i}$与${D}_{InS}^{i}$，令该期2种数据融合后的地面形变数据为Dⁱ，采用多项式曲面拟合方法作为附加系统参数，作为InSAR数据的系统误差改正项，那么对于i点的形变量计算公式为：

（5）${D}_{GNSS}^{i}$=Dⁱ ，

（6）${D}_{InS}^{i}$=Dⁱ+Aⁱ×S ，

式中：Aⁱ多项式曲面拟合的系数矩阵；S为多项式曲面拟合的系统参数矩阵。

本实验采用与监测点三维位置有关的一次多项式曲面拟合方法来作为InSAR数据的系统误差改正项，即有：

（7）Aⁱ×S=a₀+a₁Xⁱ+a₂Yⁱ+a₃Zⁱ ，

写成矩阵形式可得：

（8）Aⁱ×S=[1 Xⁱ Yⁱ Zⁱ]×$\left[\begin{array}{l}{a}_{0}\\ {a}_{1}\\ {a}_{2}\\ {a}_{3}\end{array}\right]$，

式中Xⁱ，Yⁱ，Zⁱ为点i在初始时期对应的坐标值。

式（5）和（6）可写成以下矩阵形式：

（9）$\left[\begin{array}{l}{D}_{GNSS}^{i}\\ {D}_{InS}^{i}\end{array}\right]$=$\left[\begin{array}{l}1\\ 1\end{array}\right]$Dⁱ+$\left[\begin{array}{l}0\\ {A}^{i}\end{array}\right]$S ，

其中，令：

（10）$\left[\begin{array}{l}{D}_{GNSS}^{i}\\ {D}_{InS}^{i}\end{array}\right]$=${D}_{GNSS-InS}^{i}$，$\left[\begin{array}{l}1\\ 1\end{array}\right]$=Bⁱ，$\left[\begin{array}{l}0\\ {A}^{i}\end{array}\right]$=$\overline{{A}^{i}}$，

那么对式（9）可简写成如下观测方程形式：

（11）${D}_{GNSS-InS}^{i}$=BⁱDⁱ+$\overline{{A}^{i}}$S ，

则对于n个点的观测方程有：

（12）$\left[\begin{array}{l}{D}_{GNSS-InS}^{1}\\ ︙\\ {D}_{GNSS-InS}^{n}\end{array}\right]$=$\left[\begin{array}{lll}{B}^{1}& \dots & 0\\ ︙& \ddots & ︙\\ 0& \dots & {B}^{n}\end{array}\right]\left[\begin{array}{l}{D}^{1}\\ ︙\\ {D}^{n}\end{array}\right]$+$\left[\begin{array}{l}\overline{{A}^{1}}\\ ︙\\ \overline{{A}^{n}}\end{array}\right]$S ，

式（12）的观测方程的误差方程可写为：

（13）$\underset{V}{\underset{⏟}{\left[\begin{array}{l}{V}^{1}\\ ︙\\ {V}^{n}\end{array}\right]}}$=$\underset{B}{\underset{⏟}{\left[\begin{array}{lll}{B}^{1}& \dots & 0\\ ︙& \ddots & ︙\\ 0& \dots & {B}^{n}\end{array}\right]}}$$\underset{\widehat{x}}{\underset{⏟}{\left[\begin{array}{l}{D}^{1}\\ ︙\\ {D}^{n}\end{array}\right]}}$+$\underset{A}{\underset{⏟}{\left[\begin{array}{l}\overline{{A}^{1}}\\ ︙\\ \overline{{A}^{n}}\end{array}\right]}}\underset{\widehat{S}}{\underset{⏟}{S}}$-$\underset{l}{\underset{⏟}{\left[\begin{array}{l}{D}_{GNSS-InS}^{1}\\ ︙\\ {D}_{GNSS-InS}^{n}\end{array}\right]}}$，

即可简写成如下形式^[16]：

（14）V=[B A]$\left[\begin{array}{l}\widehat{x}\\ \widehat{s}\end{array}\right]$-l ，

那么根据最小二乘平差法与附加系统参数的平差原理，可以求得$\widehat{x}$的系统改正参数A$\widehat{s}$。由误差方程根据平差法可写出其法方程。则有：

（15）$\left[\begin{array}{l}{N}_{11}　{N}_{12}\\ {N}_{21}　{N}_{22}\end{array}\right]\left[\begin{array}{l}\widehat{x}\\ \widehat{s}\end{array}\right]$-$\left[\begin{array}{l}{W}_{1}\\ {W}_{2}\end{array}\right]$=0 ，

其中N₁₁=B^TPB，N₁₂=B^TPA，N₂₁=A^TPB，N₂₂=A^TPA，W₁=B^TPl，W₂=A^TPl，P为权重矩阵。

根据式（15）可以解得：

（16）$\left[\begin{array}{l}\widehat{x}\\ \widehat{s}\end{array}\right]$=${\left[\begin{array}{l}{N}_{11}　{N}_{12}\\ {N}_{21}　{N}_{22}\end{array}\right]}^{-1}\left[\begin{array}{l}{W}_{1}\\ {W}_{2}\end{array}\right]$，

由分块矩阵求逆公式可知：

（17）

${\left[\begin{array}{l}{N}_{11}　{N}_{12}\\ {N}_{21}　{N}_{22}\end{array}\right]}^{-1}$=

$\left[\begin{array}{l}{N}_{11}^{-1}+{N}_{11}^{-1}{N}_{12}{M}^{-1}{N}_{21}{N}_{11}^{-1} -{N}_{11}^{-1}{N}_{12}{M}^{-1}\\ -{M}^{-1}{N}_{21}{N}_{11}^{-1}　　　　{M}^{-1}\end{array}\right]$，

式中：M=N₂₂-N₂₁${N}_{11}^{-1}$N₁₂。

由（16）与（17）两式能够解得：

（18）$\left[\begin{array}{l}\widehat{x}\\ \widehat{s}\end{array}\right]$=$\left[\begin{array}{l}{N}_{11}^{-1}{W}_{1}-{N}_{11}^{-1}{N}_{12}{M}^{-1}({W}_{2}-{N}_{21}{N}_{11}^{-1}{W}_{1})\\ {M}^{-1}({W}_{2}-{N}_{21}{N}_{11}^{-1}{W}_{1})\end{array}\right]$。

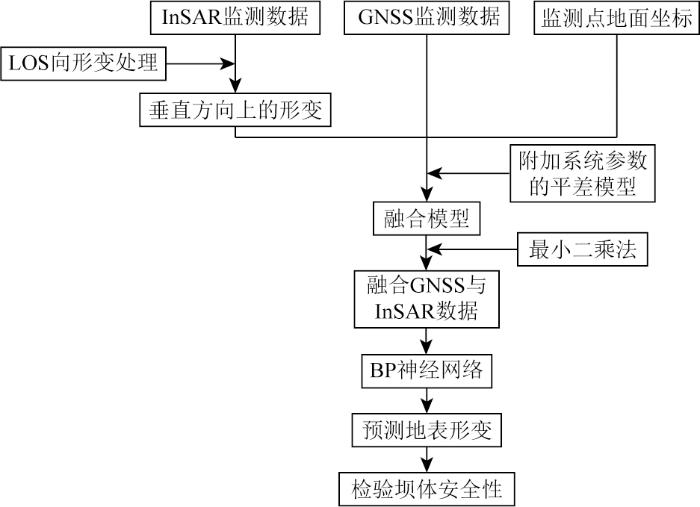
求得多项式曲面拟合的系统参数矩阵$\widehat{s}$，之后对于尾矿库坝体表面其他点的同时期InSAR监测数据，只需将其代入模型D=D_Ins-A×S即可对InSAR数据进行改正，得到修正后的点位纵向形变量，其中A为坝体表面对应监测点的三维原始坐标矩阵。图3为数据融合流程图。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 数据融合流程图

Fig.3 Data fusion flow chart

2.3 BP神经网络原理

BP神经网络包含输入层、输出层和隐含层，是一种按照反向传播（back propagation，BP）算法训练的多层前馈神经网络^[17]。这种网络的关键为BP算法，BP算法能够根据网络每次训练得到的结果与预想结果进行误差分析，进而修改网络参数的权值和阈值，逐渐得到能输出和预想结果一致的模型。BP神经网络的计算学习过程分为信号前向传播和误差反向传播2个阶段^[18]，其具有任意复杂的模式分类能力和优良的多维函数映射能力，在理论上可以拟合出任意曲面，也正是因为这一特点，使得BP神经网络成为应用最广泛的神经网络。

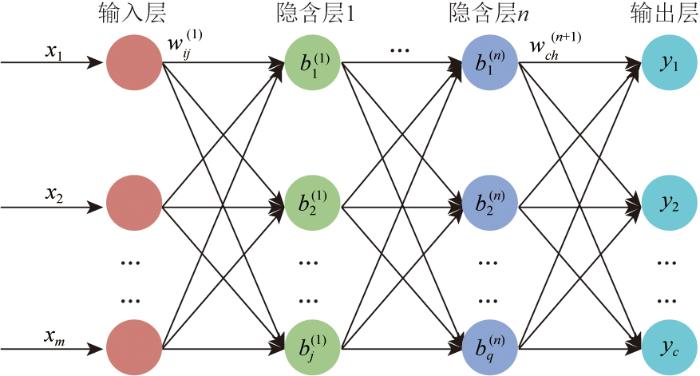
图4为BP神经网络原理模型，其中输入层用于接收外部信号，输出层产生网络最终输出，隐含层则对输入信号进行非线性变换，提取特征，输入层、输出层只有一层，一般情况下，隐含层也只有一层，但根据输入数据与输出数据的复杂程度，可以适当提升隐含层的层数及隐含层神经元个数来实现更好的拟合效果。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 神经网络结构示意图

Fig.4 Neural network structure diagram

BP神经网络的正向传播阶段计算如下：

在正向传播过程中，输入层到隐含层1的加权求和值计算公式为：

（19）${z}_{j}^{（1）}$=$\sum _{i=1}^{m}{w}_{ij}^{（1）}$x_i+${b}_{j}^{（1）}$，

之后在隐含层1中各个神经元中的值经由激活函数输出为：

（20）${a}_{j}^{（1）}$=f（${z}_{j}^{（1）}$），

隐含层1中的输出到隐含层2的加权求和值计算公式为：

（21）${z}_{k}^{（2）}$=$\sum _{p=1}^{j}{w}_{kp}^{（2）}{a}_{p}^{（1）}$+${b}_{k}^{（2）}$，

隐含层2中各个神经元中的值经由激活函数输出计算公式为：

（22）${b}_{k}^{（2）}$=f（${z}_{k}^{（2）}$），

如上述过程一直传递至最后一个隐含层n，再由最后一个隐含层将其输出经由式（22）输出到输出层：

（23）${z}_{c}^{（n+1）}$=$\sum _{h=1}^{q}{w}_{ch}^{（n+1）}{a}_{h}^{（n）}$+${b}_{c}^{（n+1）}$，

再由输出层使用激活函数输出最终值，公式为：

（24）y_c=f（${z}_{c}^{（n+1）}$），

式中：w为权重；b为偏置；x为输入值；a为中间层激活函数的输出值；y为最后由网络得到的输出值；z为加权求和值；f为激活函数（一般为sigmoid函数）。

正向传播阶段结束，网络自动进入反向传播阶段，在反向传播阶段中，神经网络会计算其训练输出值y_c与真实值y之间的误差E，计算公式为：

（25）E=$\frac{1}{2}\sum （{y}_{c}-y{）}^{2}$。

之后根据链式法则，将输出层的误差反向传递到每个隐含层，计算每个隐含层神经元的误差，再利用梯度下降法更新各层之间的权重与偏置，使得网络的输出值逼近真实值^[19-20]。然后重复正向传播与反向传播过程，直到网络训练收敛，误差达到预设阈值。

3 实验结果

3.1 数据融合结果

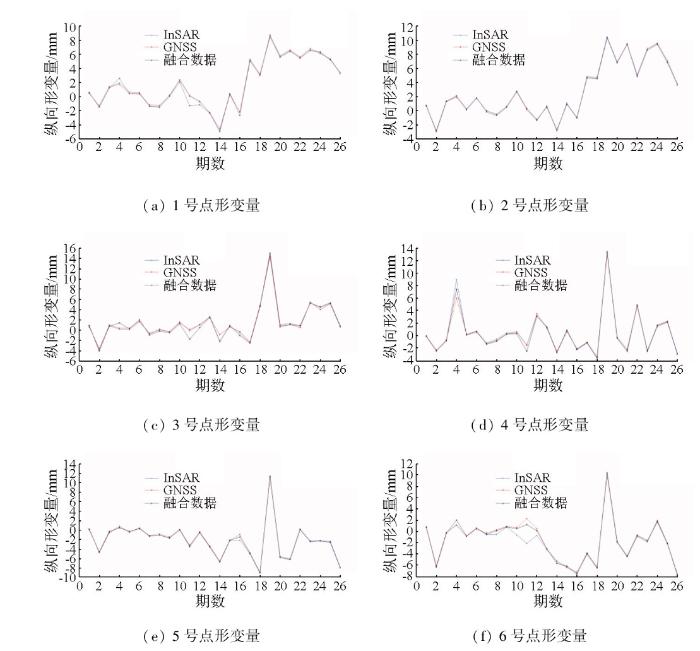
利用本实验提出的GNSS/InSAR数据融合模型对研究数据进行改正，得到融合后各点数据如表2所示，各点融合后数据与InSAR，GNSS数据对比曲线图如图5所示。

表2 各点InSAR数据与GNSS融合后的数据

Tab.2 Data after InSAR data and GNSS fusion at each point

期数	形变量/mm						期数	形变量/mm
期数	#1	#2	#3	#4	#5	#6	期数	#1	#2	#3	#4	#5	#6
1	0.637 1	0.615 5	0.979 5	-0.082 2	0.234 0	0.803 0	14	-4.956 4	-2.788 8	-2.134 8	-2.791 1	-6.699 8	-5.676 9
2	-1.460 7	-2.950 4	-3.993 2	-2.491 5	-4.643 6	-6.334 6	15	0.427 4	0.842 5	0.981 6	0.797 3	-2.098 1	-6.149 1
3	1.273 6	1.239 1	0.801 0	-0.811 3	-0.381 7	-0.333 6	16	-2.615 4	-1.124 9	-0.962 9	-2.236 6	-1.405 7	-7.558 9
4	2.658 6	2.072 8	1.490 7	7.412 5	0.520 3	2.025 0	17	5.109 2	4.628 5	-2.439 1	-1.143 9	-4.825 7	-3.887 0
5	0.474 9	0.049 4	0.335 2	0.169 2	-0.244 7	-0.795 4	18	3.069 5	4.539 3	4.668 6	-3.581 6	-8.931 5	-6.462 6
6	0.629 5	1.733 3	2.096 4	0.672 0	0.412 4	0.601 5	19	8.841 9	10.362 4	15.089 3	13.455 7	11.380 1	10.399 6
7	-1.319 0	-0.113 3	-0.880 3	-1.401 8	-1.241 2	-0.475 0	20	5.687 2	6.759 1	0.908 7	-0.348 7	-5.607 8	-1.784 0
8	-1.484 2	-0.624 5	-0.133 0	-0.926 9	-0.990 5	0.117 2	21	6.497 3	9.412 2	1.143 2	-2.409 3	-6.108 6	-4.407 3
9	0.121 5	0.494 8	-0.430 2	0.221 7	-1.595 3	0.800 5	22	5.618 1	4.864 5	0.958 5	4.878 0	0.231 5	-0.646 1
10	2.128 4	2.686 0	1.283 6	0.297 1	0.091 0	0.500 9	23	6.627 7	8.626 6	5.340 9	-2.485 7	-2.274 1	-1.678 8
11	-1.245 6	0.287 7	-1.665 7	-2.530 0	-3.448 7	1.209 5	24	6.440 3	9.453 2	4.616 0	1.632 2	-2.200 9	1.804 0
12	-1.126 7	-1.372 2	0.561 0	3.087 9	-0.439 2	0.131 3	25	5.362 4	6.862 3	5.398 5	2.257 3	-2.408 6	-2.099 4
13	-2.288 3	0.465 3	2.618 1	1.317 1	-3.416 0	-3.081 8	26	3.346 7	3.626 3	0.785 0	-2.959 6	-7.874 3	-7.624 1

新窗口打开| 下载CSV

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 融合后数据与InSAR，GNSS数据对比图

Fig.5 Fusion data is compared with InSAR and GNSS data

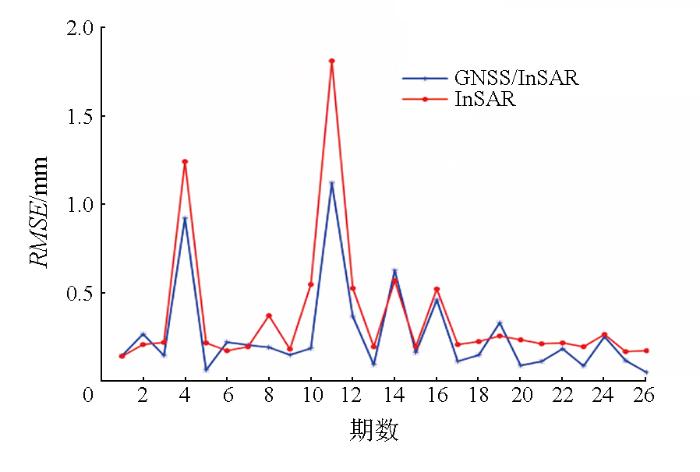
由图5能够看出，融合后数据与原始GNSS，InSAR数据分布大致相同，证明拟合效果较好，融合后数据、InSAR数据与GNSS数据间的均方根误差（root mean square error，RMSE）如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 RMSE分布图

Fig.6 RMSE distribution

通过图6融合数据（GNSS/InSAR）和InSAR的RMSE分布图可知，融合后的26期形变数据中，仅在第2期与第19期数据的RMSE高于原始InSAR数据，推测可能是由于所使用的实验数据较少所导致的，但融合后26期数据的RMSE整体上明显低于融合前数据，较融合前下降最多70.61%，平均下降25.91%，证明融合后形变数据精度更高。

本实验利用监测点原始三维坐标的一次多项式曲面拟合方法，融合InSAR与GNSS地表形变监测数据，为了该融合模型的可行性，决定在同一原始数据下，通过计算并比较本实验与王洲^[8]所提出的二维融合模型2种模型下融合数据与真实GNSS数据的残差值，来验证本实验所提改进融合模型的可行性。

残差值是预测数据与实际观测数据的差值，其能够直接反映出预测数据与真实数据之间的差距，其计算公式为：

（26）δ=y_i-${\widehat{y}}_{i}$，

式中：δ为残差值；${\widehat{y}}_{i}$为预测数据，y_i为实际观测值。

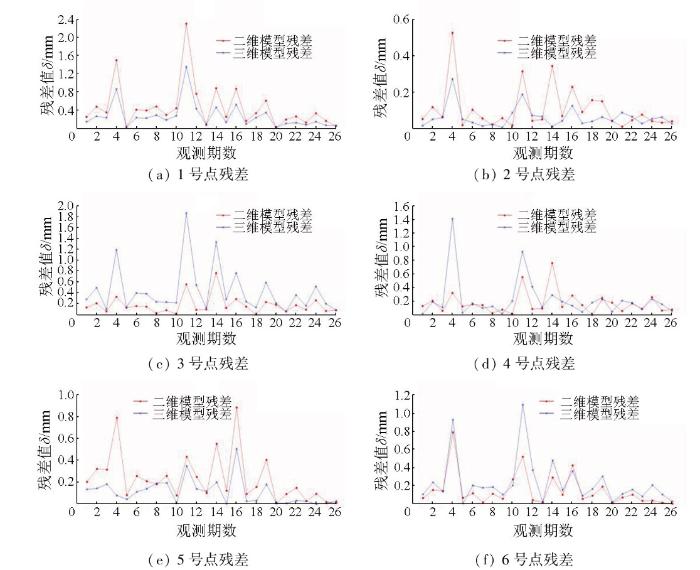
根据每个监测点26期数据的融合值与真实GNSS监测形变值计算出残差值，并取绝对值，从而对2种模型的融合效果进行评估，绘制出每个监测点26期数据的残差图如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 2种模型融合值残差图

Fig.7 Residual plots of fusion values of the 2 models

通过6个点的时序残差图可知，3号点和6号点二维模型优于三维融合模型，推测这可能是由于该2点所处尾矿库位置特殊，形变情况复杂所造成的；分析其他4个点可知，利用三维融合模型对InSAR与GNSS数据融合后，数据精度明显优于二维模型融合后数据，而考虑到坝体表面的面积宽阔性，特殊点位较少。由此可知，本文提出的三维融合模型在研究区域内是可行的。

以时间序列为单位对GNSS与InSAR数据进行融合，可以拟合出每一期融合模型中的多项式曲面拟合的系统参数矩阵S_i（i=1，2，…，26），于是，利用模型D_InSAR=D_InS-GNSS+A×S_i即可利用各点的三维坐标对InSAR监测数据进行误差改正，从而提高InSAR数据的精度。

对于多源数据建立的融合模型，可通过分析每一期拟合出的系统参数矩阵$\widehat{S}$的值并采取对其取加权平均值的方法计算出一个可通用的系统参数矩阵$\widehat{S}$，以便后续对InSAR数据进行误差改正，获取监测点的准确形变数据。

3.2 神经网络预测结果

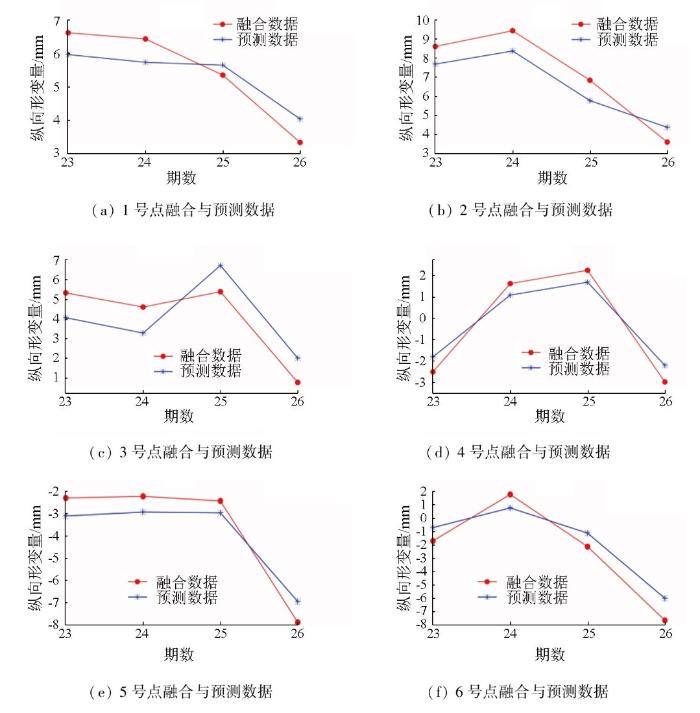
以本实验6个点26期改正后的时序形变数据为例，以点为单位，构建单隐含层BP神经网络，设置神经网络隐含层节点为4的情况下，使用purelin作为传递函数，采用梯度下降训练法，对每组数据进行归一化处理，并将处理后的数据作为训练集对神经网络进行训练，利用学习后的神经网络对各点第23~26期数据进行仿真输出，并对仿真结果进行反归一化处理，再与实际值进行比较以此测试神经网络准确性，在经过深度学习与仿真后，各点测试集的网络输出值与实际值对比曲线图如图8所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 网络输出值与融合值对比图

Fig.8 Comparison between network output value and fusion value

各点的第23~26期网络预测输出值与实际值的RMSE如表3所示。

表3 网络预测输出值与融合值的RMSE

Tab.3 RMSE of the network prediction output value and the fusion value （mm）

点号	#1	#2	#3	#4	#5	#6
RMSE	0.610 5	0.962 5	1.290 4	0.648 8	0.764 1	1.199 8

新窗口打开| 下载CSV

通过图8可知，利用神经网络虽然不能非常精准地预测出地表形变值，但整体上能很好地预测出多期地表纵向形变的形变趋势。通过网络预测输出值与融合值的均方根误差表可以看出，各点的形变预测输出值与融合值之间的RMSE值整体均保持在1.5 mm以下，最低0.610 5 mm，最高1.290 4 mm。分析可知，在神经网络经历多次训练之后，多期地表形变的形变值误差均拥有mm级别的精度，预测效果较好，因此，本研究认为，对尾矿库坝体点的InSAR利用融合模型对其进行修正后，再利用BP神经网络对其进行预测可行。

利用训练好的神经网络以最后一组数据作为输入值，仿真预测各监测点在未来第27期的竖直形变情况，预测结果见表4。

表4 由神经网络预测的第27期监测点形变值

Tab.4 Deformation value of the 27th monitoring point predicted by the neural network （mm）

点号	#1	#2	#3	#4	#5	#6
神经网络输出第27期形变数据	3.503 5	7.264 9	4.717 8	3.492 5	2.992 9	-13.474 3

新窗口打开| 下载CSV

4 结论

本文通过建立附有限制参数的平差三维数据融合模型，将获取的时序形变GNSS与InSAR数据进行融合，对InSAR数据进行误差改正以提高InSAR数据的精度，提高对尾矿库坝体整体稳定性分析精度，同时利用优化BP神经网络模型对未来形变预测进行输出并验证其可行性。

1）本文所提出附有限制参数的三维融合模型，对InSAR与GNSS数据进行融合后，在以RMSE作为精度评定标准的情况下，融合后RMSE较融合前下降最多70.61%，平均下降25.91%，对InSAR数据的改正具有较好的效果，对于形变情况复杂的少量点效果一般，总体本实验所提出融合模型适用于InSAR和GNSS数据融合。

2）同时，所采用的优化BP神经网络模型，在训练样本较少的情况下，预测结果较好，各点网络输出值与原始GNSS数据的RMSE小于1.5 mm，预测所得出的数据拥有较好的精度。

因此，本论文研究成果能够准确地对尾矿库坝体纵向形变进行监测与预测，为矿区尾矿库坝体稳定性分析及评价提供可靠的技术及数据支撑。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

李如仁, 孙加瑶.

融合SBAS-InSAR与GS-LSTM的尾矿库沉降监测与预测

[J]. 金属矿山, 2023(1):102-109.