无人机影像稳健区域网平差

doi:10.6046/gtzyyg.2020.02.06

无人机影像稳健区域网平差

薛武¹, 赵玲², 于英³

1.航天工程大学太空安全研究中心,北京 101416

2.91039部队,北京 102400

3.信息工程大学地理空间信息学院,郑州 450001

Robust bundle adjustment for UAV images

XUE Wu¹, ZHAO Ling², YU Ying³

1. Space Security Research Center, Space Engineering University, Beijing 101416, China

2. 91039 Troops, Beijing 102400, China

3. School of Geospatial Information, Information Engineering University, Zhengzhou 450001, China

责任编辑: 张仙

收稿日期: 2019-06-21 修回日期: 2020-02-5 网络出版日期: 2020-06-15

基金资助:

航天工程大学青年创新基金项目

Received: 2019-06-21 Revised: 2020-02-5 Online: 2020-06-15

作者简介 About authors

薛武(1988-),男,博士,助理研究员,研究方向为无人机摄影测量与计算机视觉。Email:xuewu_81@126.com。。

摘要

针对无人机影像区域网平差中误匹配点较多,采用方差损失函数可能造成求解参数失真,偏离真值误差大,甚至无法收敛的问题,采用了一种顾及观测值可靠性的稳健区域网平差方法。该方法采用损失函数作为粗差抑制策略,是在Cauchy损失函数基础上的一种变体,主要思想为根据特征点重叠度的均值、方差以及残差大小自适应调整总体损失函数,从而克服误匹配点对平差参数求解的干扰,并设计了不依赖地面控制点的精度评价实用方法。实验表明,该方法在较高误匹配率的情况下,仍然能够得到稳健的平差结果,具有一定实用价值。

关键词： 无人机影像 ; 误匹配点 ; 稳健 ; 损失函数

Abstract

Aimed at tackling the problems that there are many mismatched points in the bundle adjustment of unmanned aerial vehicle (UAV) images, the variance loss function may cause the distortion of the solution parameters, and there exists large deviation from the true value which even causes impossibility of converge, the authors applied a robust bundle adjustment method considering the reliability of the observation value. This method uses loss function as a strategy to suppress gross errors, and is a variant designed on the basis of Cauchy loss function. The main idea of this method is adjusting the total loss function adaptively according to the mean value and variance of overlap degree and the residual of feature points, so as to overcome the influence of mismatched points on the computation of image parameters. Correspondingly, a practical accuracy evaluation method independent of ground control point (GCP) was designed. Experiments show that the method can still get robust adjustment results with high mismatch rate, and hence it is practical.

Keywords： UAV image ; mismatch points ; robust ; loss function

PDF (5050KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

薛武, 赵玲, 于英. 无人机影像稳健区域网平差. 国土资源遥感[J], 2020, 32(2): 40-45 doi:10.6046/gtzyyg.2020.02.06

XUE Wu, ZHAO Ling, YU Ying. Robust bundle adjustment for UAV images. REMOTE SENSING FOR LAND & RESOURCES[J], 2020, 32(2): 40-45 doi:10.6046/gtzyyg.2020.02.06

0 引言

无人机影像定位过程中的“噪声”主要是指在连接点提取过程中产生的误匹配点,这些误匹配点与正确的观测值混淆在一起给光束法区域网平差造成很大干扰。采用最小二乘方法解算影像内外方位元素可以很好地配赋偶然误差,但对于影像误匹配带来的粗差却不能有效地探测和剔除,常常会将粗差点的残差配赋到其他正确的点位上,使得平差结果严重偏离真值^[1,2]。

计算机视觉中通常在特征匹配结束后,利用匹配得到的同名点采用随机抽样一致方法估计影像之间的单应矩阵或者基本矩阵,将不符合单应矩阵或者基本矩阵约束的点判定为误匹配点进行剔除^[3,4]。这种方法需要设定用于区分内外点的阈值,阈值的设定对于结果的影响较大。特别是当一批影像中误匹配点的比率有较大的浮动时,阈值的设定更加困难。摄影测量学的处理策略是在光束法平差的过程中进行粗差的探测与剔除,常用的方法有数据探测法和选权迭代法。数据探测法的理论基础是统计学中的假设检验,该方法能发现粗差,但是定位困难,且每次只能检测一个观测值。选权迭代法是在平差的过程中按依据残差选定的权函数动态调整每个观测值在下一次计算中的权值,常用的权函数有丹麦法、El-Hakim法和李德仁法等^[5,6,7,8]。然而对于无人机影像中存在较多的误匹配点的情况,选权迭代法的效果也并不理想。

无人机影像区域网平差过程中噪声数据较多,采用标准的L2范数对于噪声比较敏感,尤其是为了克服法方程的病态而采用Levenberg-Marquardt (L-M)法,噪声的影响更加明显^[9,10,11]。为此采用一种顾及观测值可靠性的稳健平差方法,根据特征点的重叠度和残差大小自适应调整代价函数,从而克服误匹配点对平差结果的干扰。

1 方法流程

无人机影像稳健区域网平差的核心思想是采用虚警值最小化的方法剔除误匹配点^[12,13],对于残留的误匹配点,则通过设计稳健的代价函数克服其对平差结果的影响。首先对无人机影像进行特征提取与匹配,然后采用虚警值最小化的方法进行误匹配剔除,接着采用稳健光束法平差,最后进行平差精度评价。

1.1 光束法平差

无人机影像的成像模型为共线条件方程^[7],设x,y为像点的像平面坐标; x₀,y₀,f为影像的内方位元素; X_S,Y_S,Z_S为摄站点的物方空间坐标; X,Y,Z为物方点的物方空间坐标; △x和△y分别为x和y方向的系统误差; a_i,b_i,c_i(i = 1,2,3)为影像的 3 个外方位角元素组成的 9 个方向余弦,则

(1)

\{\begin{array}{l} x - x_{0} + △ x = - f \frac{a_{1} (X - X_{S}) + b_{1} (Y - Y_{S}) + c_{1} (Z - Z_{S})}{a_{3} (X - X_{S}) + b_{3} (Y - Y_{S}) + c_{3} (Z - Z_{S})} \\ y - y_{0} + △ y = - f \frac{a_{2} (X - X_{S}) + b_{2} (Y - Y_{S}) + c_{2} (Z - Z_{S})}{a_{3} (X - X_{S}) + b_{3} (Y - Y_{S}) + c_{3} (Z - Z_{S})} \end{array}

。

光束法平差的基本数学模型也是共线条件方程。由于影像坐标观测值是未知数的非线性函数,因此需要进行泰勒展开,对观测方程线性化处理得到误差方程,即

(2)

\{\begin{array}{l} v_{x} = c_{11} d X_{S} + c_{12} d Y_{S} + c_{13} d Z_{S} + c_{14} d φ + c_{15} d ω + c_{16} d κ + c_{17} d X + c_{18} d Y + c_{19} d Z - l_{x} \\ v_{y} = c_{21} d X_{S} + c_{22} d Y_{S} + c_{23} d Z_{S} + c_{24} d φ + c_{25} d ω + c_{26} d κ + c_{27} d X + c_{28} d Y + c_{29} d Z - l_{y} \end{array}

式中c_ij(i=1,2; j=1,2,…,9)为代价函数对待求参数的导数,dX_S,dY_S,dZ_S,dφ,dω,dκ,dX,dY,dZ为待求参数的改正数; l_x和l_y分别为利用当前内外方位元素得到的像方坐标、与观测值的差值。以矩阵的形式表示为,

(3)V=AX-L ,

式中: V=(v_x,v_y)^T; X=(dX_S,dY_S,dZ_S,dφ,dω,dκ,dX,dY,dZ)^T; A= $(\begin{array}{l} c_{11}, c_{12}, c_{13}, c_{14}, c_{15}, c_{16}, c_{17}, c_{18}, c_{19} \\ c_{21}, c_{22}, c_{23}, c_{24}, c_{25}, c_{26}, c_{27}, c_{28}, c_{29} \end{array})$ ; L=(l_x,l_y)^T。

误差方程通常采用最小二乘的方法来解算,最小二乘法的目标函数为:

(4)minV^TPV ,

式中: P为观测值的权矩阵。误差方程的法方程为:

(5)A^TPAX=A^TPL ,

法方程的解为:

(6)X=(A^TPA)^-¹A^TPL 。

最小二乘估计采用的代价函数是一种L2范数,当观测值中的噪声服从高斯分布时,最小二乘估计等效于最大似然估计^[9,10]。

1.2 稳健光束法平差

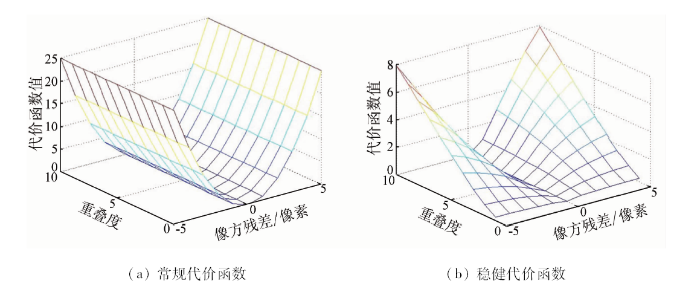
无人机影像光束法平差解决的是非线性优化问题,解决该问题的方法很多,L-M法是比较经典的一种。其本质上是一种启发式的阻尼高斯牛顿法,被广泛用于非线性估计。通过启发式方法,算法在高斯牛顿法和梯度下降法之间灵活地切换,这样既能保证算法的收敛性,又具有较快的收敛速度。但是L-M法对于输入数据中的噪声十分敏感,甚至一个错误点就会影响整体的解算精度,这些噪声可能会使L-M法陷入局部最优解或者不收敛^[9,10]。

对于无人机影像而言,连接点数量十分多,且难以避免含有噪声数据,不宜采用L-M方法。通常的做法是,在进行光束法平差之前,对数据中的噪声点进行剔除。但即便采用虚警值最小化的误匹配剔除方法也不能保证数据中的粗差被完全剔除,因此需要一种顾及观测值可靠性的稳健平差方法^{[12,13,14,15,16]}。

考虑到在影像匹配时,多度同名点具有更高的可靠性,因为特征点的重叠度越高,说明其稳定性较好,平差时可以给予更高的“信任”。所以需要一种能够顾及特征点重叠度的代价函数,以提高区域网平差的稳健性。本文采用了一种结合Cauchy理论和连接点重叠度的稳健代价函数,Cauchy代价函数和本文函数分别为:

(7)ρ(s)=log(1+s²) ,

(8)ρ_j(s_j,r_j,μ,σ)=

{(\frac{r_{j}}{μ + σ})}^{2}

log(1+

{(\frac{μ + σ}{r_{j}})}^{2} s_{j}^{2}

) ,

式中: s_j为第j个物方点的像方反投影误差; r_j为其重叠度; μ和σ分别为测区中连接点重叠度的均值和方差。对于某一物方点的重叠度,通过除以均值和方差的和实现归一化,然后取平方得到的结果作为稳健代价函数的权重。较高的重叠度说明连接点在影像上出现的轨迹较长,可靠性更高,相应的观测值被赋予更高的权重,因此稳健光束法区域网平差的目标函数可以表示为:

(9)

\min_{R_{i}, t_{i}, X_{j}} \overset{N_{C}}{\sum_{i = 1}} \overset{M_{3 D}}{\sum_{j = 1}}

ρ(‖x_ji-g(X_j,R_i,t_i,K_i)‖,r_j,μ,σ) ,

式中: M_3D为连接点的个数; N_C为每个连接点的重叠度; R_i,t_i,K_i分别为第i幅影像的外方位角元素矩阵、线元素矩阵和内方位元素矩阵; x_ji和X_j分别为特征点的像方和物方坐标观测值; g()为根据共线条件方程计算得到的像方坐标理论值。

为了更直观地展示稳健代价函数与常规代价函数的区别,以重叠度均值为3,方差为2为例,将相同数据采用不同代价函数用曲面图进行表示(图1)。从图1中明显可以看出: 对于重叠度比较低、可靠性较差的连接点,当其残差较大时,稳健代价函数能够较好地克服其影响,降低其在平差中的干扰作用; 而对于重叠度较高、可靠性也较高的点,则赋予其较高的权重,在平差中发挥更大的作用。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 代价函数曲面图

Fig.1 Surface graph of cost function

采用新的代价函数后,目标函数解算的过程变得复杂,本文利用开源库Ceres Solver对式(9)进行求解。Ceres Solver是由谷歌公司推出的解决非线性最小化问题的开源软件包,由于功能强大而稳定,在谷歌的多款产品中取得了成功的应用^[17]。

1.3 精度评价

区域网平差精度的评价通常采用2种方式: 当有地面控制点数据时,采用平差优化后的内外方位元素前方交会得到物方坐标,与外业测量结果进行比较; 当没有地面控制点时,统计平差后连接点像方残差中误差。前者得到的精度是“外符合”精度,结果客观,说服力强,但依赖于外业控制点; 后者方便灵活,只需要在平差结束之后进行一次统计运算,得到的精度结果是“内符合”精度。

为了对稳健区域网平差结果的精度进行评价,需要相对应的技术方法。由于无人机作业时很多情况下无法布设地面控制点,特别是在沙漠、海岛礁等困难地区,所以要采用一种不依赖于地面控制点的精度评价方法。采用稳健代价函数后,虽然克服了粗差点对于平差结果的影响,但并没有进行粗差的定位与剔除,所以采用统计像方残差中误差的方式也不再合适。考虑到区域网平差起的作用是对影像的内外方位元素进行“精化”,所以从这个角度出发,利用平差后的内外方位元素计算基本矩阵F,根据基本矩阵的精度间接评价区域网平差的效果。

对极几何(图2)是计算机视觉中描述两视图几何的重要概念,通常用基本矩阵F表示,本质上是同名点位于同名核线,是一种一维约束。它表征的是针孔相机成像时,两视图之间内在的几何约束^[18,19,20],即同名点坐标满足对极几何约束。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 对极几何示意图

Fig.2 Polar geometry diagram

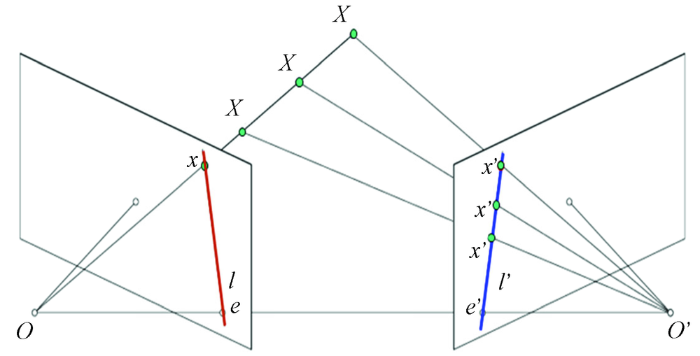
如果一个物方点在2幅影像中的齐次坐标分别为x和x',那么像点满足关系

(10)x'Fx=0 。

影像匹配结束后利用同名点坐标计算基本矩阵,根据式(10),至少需要8对同名点才能计算F,当同名点数量更多时可以对F进行最小二乘估计。在区域网平差之后,也可利用2幅影像的内外方位元素直接求解F^[19^-^20],即

(11)F=

{R^{T}}_{1}

B_[_x_]R₂ ,

式中: R₁和R₂分别为左像和右像的旋转矩阵; B_[_x_]为摄影基线向量B的叉乘矩阵表示,即

(12)B_[_x_]=

[\begin{array}{l} 0 & - B_{Z} & B_{Y} \\ B_{Z} & 0 & - B_{X} \\ - B_{Y} & B_{X} & 0 \end{array}]

式中B_X,B_Y,B_Z分别为B在各个方向上的分量。

采用了新的精度评价指标,就可以在区域网平差结束后,从测区中均匀选取一定数量的立体像对,利用平差前和平差后的内外方位元素分别求解基本矩阵。在立体像对左像上选择一定数量显著的特征点(例如地物角点、端点、交叉点等),分别利用2个基本矩阵计算核线,然后在右像上量测同名特征点到2个核线的距离,依据距离中误差大小来衡量平差前后外方位元素的精度。

2 实验与分析

实验共采用了4组不同区域的无人机影像,基本信息如表1。其中区域A,C,D数据利用固定翼无人机获取,区域B数据利用无人直升机获取,4组数据的航高在150~ 700 m范围内,数据种类较为丰富,比较具有代表性。

表1 实验数据基本情况

Tab.1 Basic information of experimental data

区域	影像数量/幅	平台	相机	像幅/像素	航摄时间	行政区划	航高/m	地面分辨率/cm
A	1 209	智能鸟无人机	Canon EOS 5DS	8 688×5 792	2015年10月	内蒙古自治区	700	10.0
B	186	无人直升机	Phase One IQ180	10 328×7 760	2015年10月	河南省	500	5.0
C	563	天宝无人机	SONY_α5100	6 000×4 000	2016年4月	河南省	150	4.0
D	433	天宝无人机	SONY_α5100	6 000×4 000	2016年4月	河南省	150	4.0

新窗口打开| 下载CSV

实验时,首先分别用常规的光束法平差和稳健区域网平差方法处理4组影像; 然后分别向4组影像中添加5%,10%,15%,20%,25%的随机噪声(通过产生随机数的方式对影像上正确匹配的同名点坐标值添加噪声,均值3像素,方差2像素,服从高斯分布),验证所提出方法的有效性。

由于实验区域没有相应的地面控制点信息可以参考,所以采用1.3中精度评价方法对稳健区域网平差的结果进行评价,统计不同方法得到的外方位元素计算出核线残差中误差,结果如表 2所示,表2中,BA表示采用选权迭代法进行光束法平差方法得到的结果,RBA表示本文提出的方法得到的结果; “×”表示处理失败。

表2 数据处理结果

Tab.2 Data processing result

区域	同名点数量 (物方/像方)	原始数据		5% 噪声		10% 噪声		15% 噪声		20% 噪声		25% 噪声
区域	同名点数量 (物方/像方)	BA	RBA	BA	RBA	BA	RBA	BA	RBA	BA	RBA	BA	RBA
A	68 238/141 592	1.03	0.71	2.32	0.76	4.68	0.81	×	1.33	×	1.50	×	2.84
B	532 324/2 309 275	0.99	0.58	1.21	0.66	3.25	0.72	×	1.29	×	2.01	×	×
C	206 543/454 724	1.23	0.72	1.56	0.84	6.22	0.88	×	1.56	×	2.34	×	2.99
D	330 087/742 503	1.35	0.78	3.11	0.77	5.88	0.98	×	1.07	×	1.12	×	×

新窗口打开| 下载CSV

通过分析表 2可以得出以下结论: ①常规的光束法平差对于噪声比较敏感,当数据中噪声达到5%时,平差精度显著下降,当噪声达到10%时,平差结果精度超出可以接受的范围,噪声比例达到15%以上时,平差不收敛,解算失败; ②本文所设计的代价函数对于噪声具有一定的稳健性,当噪声比例低于10%时,平差结果几乎不受影响,当噪声比例达到20%时,精度变差,但仍然可以解算,当噪声比例大于20%时,不一定能够解算出结果。

实验结果表明,稳健代价函数能够有效克服噪声的影响,在无人机数据处理中可以提升区域网平差的稳健性,具有一定的实用价值。采用稳健区域网平差得到的稀疏点云如图3所示,点云的分布情况可以间接说明平差结果的质量,通过道路、建筑物的几何轮廓的比例协调性和连续性可以看出鲁棒区域网平差得到的加密点质量较好。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 稀疏点云

Fig.3 Sparse point cloud

3 结论

1)本文采用了一种顾及观测值可靠性的稳健平差方法,根据特征点的重叠度和残差大小自适应调整代价函数,从而克服误匹配点对平差结果的干扰。与稳健代价函数相对应,设计了一种区域网平差精度评价方法。

2)利用4组无人机影像进行实验,结果表明本文方法稳健性较好,能够在误匹配点比较多的情况下取得较好的结果,具有一定的实用价值。

3)本文方法可以作为传统光束法平差中粗差剔除方法的重要补充,在影像同名点匹配结果中含有较多噪声的情况下使用。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Colomina

, Molina

Unmanned aerial systems for photogrammetry and remote sensing:A review

[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2014,92:79-97.