自然资源遥感, 2022, 34(2): 37-46 doi: 10.6046/zrzyyg.2021214

技术方法

基于空间统计学的高光谱遥感影像主成分选择方法

孙肖,1, 彭军还,2, 赵锋3, 王晓阳1, 吕洁2, 张登峰4

1.中国地质调查局廊坊自然资源综合调查中心,廊坊 065000

2.中国地质大学(北京)土地科学技术学院,北京 100083

3.中国地质调查局乌鲁木齐自然资源综合调查中心, 乌鲁木齐 830057

4.中国地质调查局西安矿产资源调查中心,西安 710100

Principal component selection method for hyperspectral remote sensing images based on spatial statistics

SUN Xiao,1, PENG Junhuan,2, ZHAO Feng3, WANG Xiaoyang1, LYU Jie2, ZHANG Dengfeng4

1. Langfang Natural Resources Comprehensive Survey Center, China Geological Survey, Langfang 065000, China

2. School of Land Science and Technology, China University of Geosciences (Beijing), Beijing 100083, China

3. Urumqi Natural Resources Comprehensive Survey Center, China Geological Survey, Urumqi 830057, China

4. Xi’an Center of Mineral Resources Survey, China Geological Survey, Xi’an 710100, China

通讯作者: 彭军还(1964-),男,博士,教授,主要从事测绘理论研究。Email:pengjunhuan@163.com。

责任编辑: 李瑜

收稿日期: 2021-07-14   修回日期: 2021-12-8  

基金资助: 中国地质调查局项目“京津冀廊坊地区生态修复支撑调查”(DD20208073)

Received: 2021-07-14   Revised: 2021-12-8  

作者简介 About authors

孙 肖(1988-),男,硕士,助理工程师,主要从事高光谱遥感解译研究。Email: sunxiao@mail.cgs.gov.cn。

摘要

主成分分析是一种广泛使用的高光谱遥感影像降维方法,在面向任务的工作中,基于累计方差贡献率的主成分选择方法效果并不理想。针对主成分分析变换后主成分选择的问题,提出基于空间统计学的主成分选择方法。计算各主成分的半变异函数参数变程、拱高、基台值,综合变程和拱高/基台值实现主成分的选择。变程的大小用以判断每一个主成分空间相关性的范围,拱高/基台值的大小用以判断每一个主成分空间相关性的强弱。仿真实验证明了变程和拱高/基台值可以有效表达高光谱遥感影像空间相关性的范围和强弱。在真实高光谱遥感影像实验的基础上,从主观和客观2个方面来综合确定主成分选择的经验阈值,即变程为2.5、拱高/基台值为0.2。从基于支持向量机算法的分类结果来看,和传统方法相比,利用变程和拱高/基台值可以筛选出图像质量较好的主成分,不仅能够达到降维的目的,同时能够保证足够高的分类精度。

关键词： 高光谱; 主成分分析; 空间统计学; 半变异函数; 支持向量机

Abstract

The principal component analysis is a widely used method for dimensionality reduction of hyperspectral remote sensing images. In task-oriented work, the principal component selection method based on cumulative variance contribution rate is not ideal. To address the problem of principal component selection after principal component analysis transformation, a method of principal component selection based on spatial statistics is proposed. The selection of principal components is performed by calculating the values of the semi-variogram parameter range and partial sill/sill of each principal component. The magnitude of a range is used to judge the range of spatial correlation of each principal component, and the partial sill/sill is used to judge the strength of spatial correlation of each principal component. The simulation proves that the variable range and partial sill/sill can effectively express the range and strength of spatial correlation of hyperspectral remote sensing images. Based on the experiment of real hyperspectral remote sensing images, the empirical threshold of principal component selection is determined from subjective and objective aspects, that is, the range is 2.5, and the partial sill/sill is 0.2. According to the classification results based on the support vector machine algorithm, compared with traditional methods, the principal components with better image quality can be screened by using variable range and partial sill/sill, which can not only achieve the purpose of dimensionality reduction, but also ensure high classification accuracy.

Keywords： hyperspectral; principal component analysis; spatial statistics; semi-variogram; support vector machine

PDF (10623KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

孙肖, 彭军还, 赵锋, 王晓阳, 吕洁, 张登峰. 基于空间统计学的高光谱遥感影像主成分选择方法[J]. 自然资源遥感, 2022, 34(2): 37-46 doi:10.6046/zrzyyg.2021214

SUN Xiao, PENG Junhuan, ZHAO Feng, WANG Xiaoyang, LYU Jie, ZHANG Dengfeng. Principal component selection method for hyperspectral remote sensing images based on spatial statistics[J]. Remote Sensing for Land & Resources, 2022, 34(2): 37-46 doi:10.6046/zrzyyg.2021214

0 引言

在面向任务的高光谱遥感影像数据分析中,由于高光谱遥感影像波段数相对比较多,庞大的数据量给后续的分析处理带来了极大的挑战。在高光谱分类中,把分类精度随着波段数量的增加先升高后降低的现象叫作“Hughes”现象[1]。Chang[2]研究发现最高有94%的波段是可以舍弃的,而且不会影响分类的精度。因此,在高光谱遥感影像的研究中,一般会首先进行降维处理,主成分分析(principal component analysis,PCA)就是一种常用的线性降维方法[3]。

PCA将数据的方差作为线性变换的标准,因此,一般按照变换后数据的累积方差进行主成分的选择。降维主要的目的就是降低数据维数的同时,尽可能保留信息,而选择方差较大的主成分必然会带来信息的损失。目前没有一种有效的方法来决定该选择哪个主成分。

Jolliffe[4]通过大量实验研究将PCA变换后主成分选择的经验阈值定为累计方差贡献率大于0.85,但是该阈值在高光谱遥感的研究中具有局限性。PCA在高光谱遥感领域的应用主要包含两大类: 一类是应用于解混、变化检测、数据压缩、目标探测、去噪等的研究中,根据研究的目的和内容不同,一般选择某一特定主成分或某几个主成分进行研究[5⇓⇓⇓⇓-10]; 另一类是应用于分类研究,Chang等[11]认为利用累计方差贡献率大于0.99的主成分进行分类研究效果比较好。Li等[12]认为累计方差贡献率大于0.9就能保证分类精度大于0.85。臧卓等[13]对高光谱遥感影像降维后的主成分进行分类测试,发现累计方差贡献率与分类精度没有必然联系,而主成分的个数对分类结果的影响较为明显,认为保留前15~20个主成分较为合适。黄鸿等[14⇓-16]认为可以给定一定数量的主成分进行分类。臧卓等[17⇓-19]逐次增加主成分数量进行分类,根据分类精度确定合适的主成分个数,该方法虽然能保证分类精度最高,但是效率较慢。Mather等[20]指出不能仅依靠特征值对应的主成分来做图像分类,还应考虑图像的实际视觉效果。Rodarmel等[21]分别采用编号1—5、1—10、1—25、1—50的主成分分段计算了分类的精度,认为可以用5%~10%的主成分个数进行分类。Ibarrola-Ulzurrun等[22]将常用的主成分选择方法分为4类(基于特征值、纹理特征、类别变换和感兴趣区分离),分别利用前2,5,10,15,20主成分对这4类方法的分类精度进行了对比研究,认为特征值不是最适合的主成分选择方法,类别变换和感兴趣区分离需要人为的确定感兴趣区,因此纹理特征是比较适合的主成分选择方法,典型的纹理特征指标即信息熵。

以上主成分选择方法虽然取得了一定的效果,但是仍存在依据不充分、效率较低、主观性较强的问题。而且,PCA变换结果不随噪声排列,方差也不能判断噪声的大小。以上方法会导致部分图像质量较好的主成分被舍去,而部分图像质量较差的主成分参与分类的现象。从实际应用来看,编号较大的一些主成分对分类结果也有一定的影响[23]。

目前,定量的PCA变换后主成分选择方法的研究还比较少。Zheng等[24]提出 GA-Fisher算法,能有效地增加编号较大的有效主成分。Zhang等[25]利用免疫克隆选择算法对主成分进行二次处理,提出ICSA-PCA算法,在一定程度上解决了以上存在的问题。本文从空间统计学的角度,利用高光谱遥感影像的空间相关性,提出了一种定量的主成分选择方法。

1 研究方法

空间统计学是建立在相邻地理单元存在某种联系的基本假设之上的统计学,将统计学和现代图形计算技术结合起来,用直观的方法展现空间数据中所隐含的空间分布、空间模式以及空间相互作用等特征[26]。地统计学是空间统计学的重要组成部分,而半变异函数理论是地统计学处理空间数据的方法,是探索展布于空间并呈现出一定的随机性和结构性的自然现象的重要技术和方法,被用于描述空间相关性[27]。数据空间分布的相关性越大,即空间上聚集分布的现象越明显。若所测值不表现出任何空间依赖关系,那么,这一变量表现出空间不相关性或空间随机性。

变程、基台值、块金值是常用的表达空间自相关性的半变异函数基本参数。变程的大小反映了区域化变量影响范围的大小,或者说反映该变量的自相关尺度。在变程距离之内,空间上越靠近在一起的点之间的相关性越大,相隔距离大于变程的点之间没有自相关性。基台值与块金值之差表示由于采样数据中存在空间自相关性引起的方差变化范围,反映了数据的随机性,称为拱高。拱高和基台值的比值可以反映数据空间相关性的强弱[28-29]。利用空间数据的以上特性可以很好地研究主成分选择的问题。

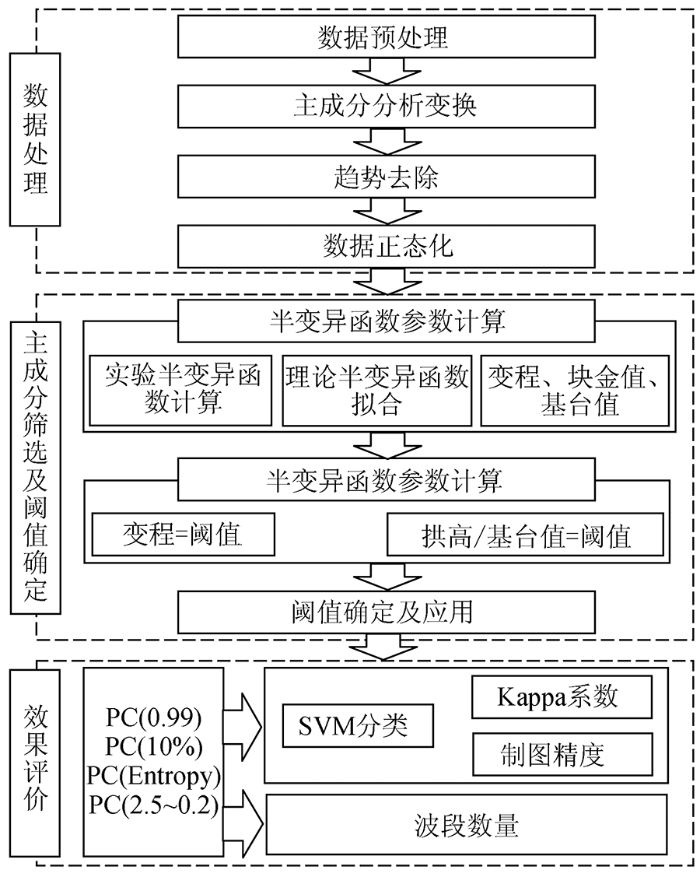
本文利用变程、拱高/基台值两个半变异函数参数进行PCA后主成分的选择,结合以上原理,基于空间统计学的高光谱遥感影像主成分选择流程见图1,主要过程如下:

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   算法流程图

Fig.1   Flowchart of algorithm


1)对高光谱遥感影像数据集进行PCA变换,获取主成分。在去除各主成分的趋势项影响后对各主成分数据进行正态化转换。

2)选定理论半变异函数模型对计算出的各主成分的实验半变异函数进行拟合,从而获取各半变异函数参数变程、基台值、块金值,由此计算出用于主成分选择的变程、拱高/基台值两个参数。

3)联合变程、拱高/基台值进行主成分选择,结合高光谱遥感影像实验结果,从主观和客观两个方面来综合确定主成分选择的经验阈值。

4)利用支持向量机(support vector machine,SVM)算法进行分类,通过分类的Kappa系数、制图精度、选择的波段数等评价主成分选择方法的效果[30-31]。与3种传统选择主成分的方法进行比较,评价本文提出的方法的好坏。

2 实验及其结果分析

2.1 仿真实验

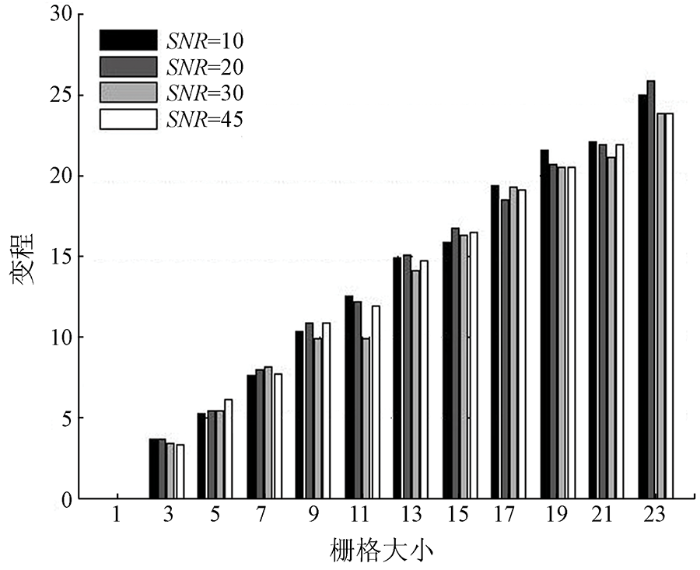
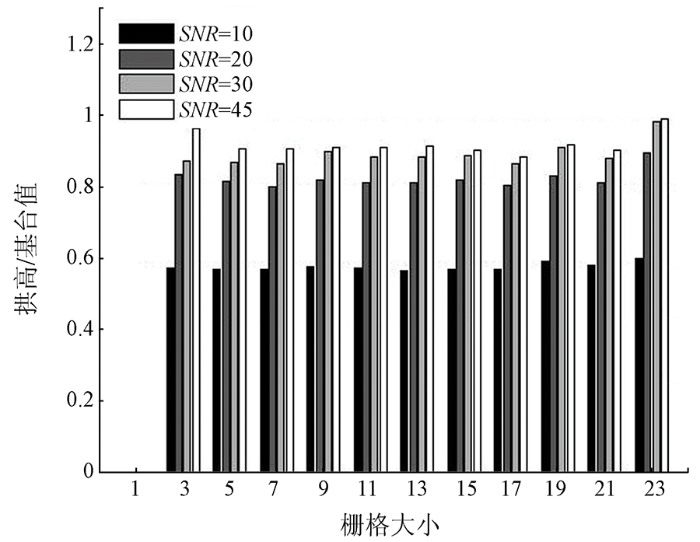
为便于研究,仿真数据大小设计为72×72。从美国地质调查局网站提供的地物波谱库里随机选择4类地物波谱,按照规则格网设计仿真图像(格网大小W=1,3,…,23)。为更加接近真实数据情况,添加信噪比分别为10,20,30,45的零均值高斯噪声(图2)。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   仿真图像(不同栅格大小W=1,3,…,23; 信噪比SNR=10,20,30,45)

Fig.2   Simulation images (different grid sizes W=1,3,…,23; SNR=10,20,30,45)


如图3、图4所示,当W=1时,即相邻的像元均为不同地物,图像以随机性为主,实验半变异函数主要表现为块金值。当W=3,5,…,23时,图像的变程计算结果与设计的网格大小基本一致,反映了图像空间相关性的范围大小。拱高/基台值计算结果受噪声影响比较明显,可以作为利用变程选择主成分的辅助参数。仿真实验从数据的空间相关性和随机性两个方面验证了利用半变异函数参数拱高/基台值、变程进行PCA后主成分选择的有效性。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   不同栅格大小仿真图像计算的变程结果

Fig.3   Results of the range of the simulation image


图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   不同栅格大小仿真图像计算的拱高/基台值结果

Fig.4   Results of the partial sill/sill of the simulation image


2.2 实际数据

2.2.1 实验数据集

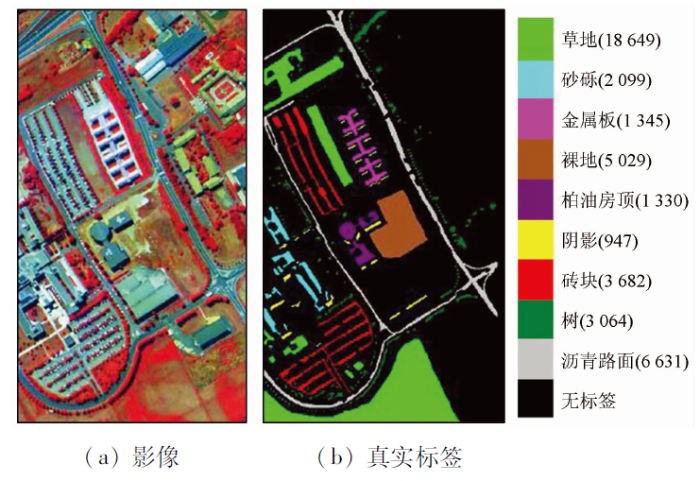
Indian Pines高光谱数据集是1992年由AVIRIS传感器获取的印第安纳州西北部农业区的高光谱遥感影像数据的一部分,图像大小为145×145像素,包含16类地物(图5)。AVIRIS数据光谱范围为0.4~2.45 μm,共224个波段,空间分辨率20 m。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   Indian Pines数据集

Fig.5   Indian Pines data set


ROSIS传感器于2003年在意大利的北部Pavia大学获取了2幅高光谱影像,University高光谱数据是该数据集的其中之一(图6)。图像大小为610×340 像素,空间分辨率1.3 m,包含9类地物。ROSIS传感器共103个波段,光谱范围为0.43~0.86 μm。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   Pavia U数据集

Fig.6   Pavia university data set


Salinas高光谱数据集由AVIRIS传感器获取的美国加利福尼亚州萨利纳斯山谷区域。图像大小为512×217像素,空间分辨率3.7 m,包含224个波段,该数据集地物类别包含16类(图7)。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   Salinas数据集

Fig.7   Salinas data set


研究中使用的Indian Pines,Pavia University(简写为Pavia U)和Salinas3种高光谱数据集获取网站网址如下: http://www.ehu.eus/ccwintco/index.php?title=Hyperspectral_Remote_Sensing_Scenes。

2.2.2 数据处理及结果

数据处理主要包含无信息波段的剔除、趋势项去除、数据正态化、实验半变异函数计算、理论半变异函数拟合等过程。

由于受水汽影响,Indian Pines数据集部分波段的成像效果比较差,本数据集中剔除的波段为104~108,150~163,220。同样,Salina数据集剔除108~112,154~167,224波段。通过二阶数据漂移估计,消除趋势项影响。空间统计学中一般都假设数据是服从正态分布,本文在正态检验的基础上,采用常态得分变换(normal score transform,NST)方法进行数据正态化的转换,该方法相比传统方法不受数据负值的影响[32]。

对于高光谱遥感影像的实验半变异函数的计算,一般是分别计算图像的0°,45°,90°和135°方向的实验半变异函数曲线,研究其曲线变化特征,通过套和获取最终的实验半变异函数。选择5种常用的模型——球状模型、指数模型、高斯模型、线性有基台值模型和普通线性模型模型,采用线性规划法进行拟合,最终,选择交叉验证结果最佳的一个作为最终的理论模型[33-34]。一般采用交叉验证后判定系数R2较大,或者残差标准差较小的理论模型作为最终结果。实验中采用判定系数R2和残差标准差的比值作为理论模型的选择标准。半变异函数参数计算结果如图8所示,为便于图面表达,图示中舍弃了拱高/基台值小于0.05的无意义主成分。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   真实数据半变异函数参数计算结果图

Fig.8   The results of the semi-variogram parameters of real data


2.2.3 主成分选择方法

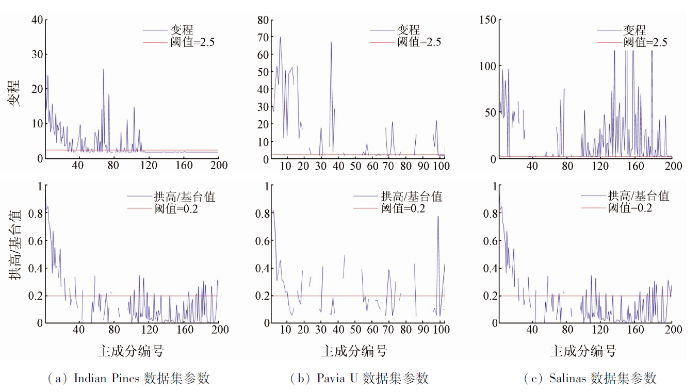
从变程、拱高/基台值的计算结果来看(图8),高光谱遥感影像PCA变换后编号较大的主成分主要表现为随机噪声,结果主要体现为块金值,该特征与仿真实验比较一致,主成分选择中舍弃该类主成分。单独利用变程或者拱高/基台值也可以进行主成分的筛选,但是对于编号较大的主成分计算出的无意义结果不能很好的判断。同时,变程和拱高/基台值的结果具有明显的互补性,对于一些无意义结果,同时通过2组参数可以有效的进行剔除。因此,本文提出综合利用以上2组参数进行主成分选择的思路。

2.2.4 阈值确定

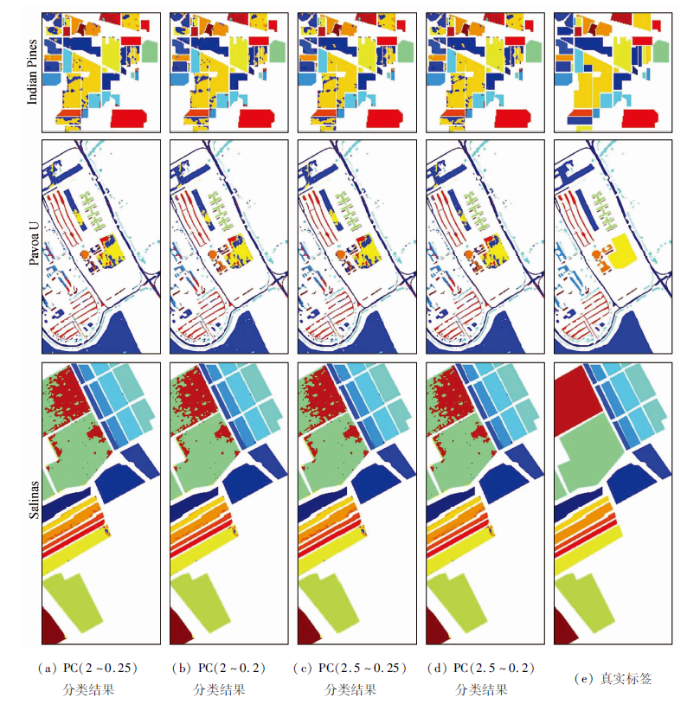
利用变程、拱高/基台值选择主成分关键的问题就是阈值的确定。通过仿真实验可以知道,图像最小的空间相关性范围大小为2,即相邻像元是相关的,也就是变程为2。为便于研究,将变程增加到2.5作为对比实验。拱高/基台值体现了图像的随机性,一般认为当该值小于0.2~0.25时,数据表现为强的随机性。为了便于研究,分别采用拱高/基台值为0.2和0.25进行对比研究。在此基础上,分别测试了变程=2、拱高/基台值=0.2(表示为PC(2~0.2)); 变程=2、拱高/基台值=0.25(表示为PC(2~0.25)); 变程=2.5、拱高/基台值=0.2(表示为PC(2.5~0.2)); 变程=2.5、拱高/基台值=0.25(表示为PC(2.5~0.25))的主成分选择效果。

为了说明利用几种阈值进行主成分选择的效果,从主观和客观2个方面进行评价。主观评价方法即观察利用几种阈值选择出的主成分的图像质量。以Indian Pines数据集为例,图9为该数据集PCA变换后各主成分的缩略图,表1为不同阈值筛选的主成分。图9中排列顺序为从左至右,从上至下,主成分编号依次增大,表示为PC1,PC2,…,PC200。实验中发现,无论哪种阈值组合都可以剔除图面质量较差的PC9。当拱高/基台值固定时,增大变程会剔除更多的主成分。从表1结果来看,当拱高/基台值=0.25时,PC103被剔除,同时,当变程由2增加到2.5会导致PC108,PC109被剔除。从图9来看,PC103,PC108,PC109主成分的图像细节仍然比较清楚。当变程固定时,减小拱高/基台值会增加更多主要表现为随机性的主成分。从表1结果来看,当变程=2时,拱高/基台值由0.25减小到0.2会将PC22,PC29,PC55,PC59,PC103筛选进来。从图9来看,PC22,PC29,PC59,PC103图像细节仍然比较清楚,但是PC55图像质量较差。因此还不能完全说明拱高/基台值的阈值确定为哪个比较合适。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   Indian Pines数据集PCA后各主成分缩略图

Fig.9   Thumbnails of each principal component after the PCA transformation of the Indian Pines data set


表1   Indian Pines数据集不同阈值筛选的主成分

Tab.1  Principal component selected by different thresholds in Indian Pines data set

不同方法筛选的主成分编号
PC(2~0.25)1~8,10~21,23~25,28,38,66,68,88,92,101,108,109
PC(2~0.2)1~8,10~25,28,29,38,55,59,66,88,92,101,103,108,109
PC(2.5~0.25)1~8,10~21,23~25,28,38,66,68,88,92,101
PC(2.5~0.2)1~8,10~25,28,29,38,59,66,68,88,92,101,103

新窗口打开| 下载CSV


客观评价方法是计算所选择的主成分分类的Kappa系数进行对比评价。本文利用常用的SVM方法对几种阈值的筛选结果进行分类,分类过程通过ENVI软件实现,利用RBF核,设置gamma=0.1,penalty=100。利用几组阈值选择的主成分进行分类,从表2的分类精度结果来看均能得到较高的分类精度,从图10的分类效果来看结果差别不明显。综合考虑主观评价结果,利用PC(2~0.2)筛选出的主成分较多,利用PC(2.5~0.25)筛选出的主成分较少,PC(2.5~0.2)总体分类精度较高,因此,最终选择变程=2.5,拱高/基台值=0.2作为主成分选择的阈值。

表2   不同阈值的Kappa系数

Tab.2  Kappa coefficient of different thresholds

数据集PC
(2~0.25)		PC
(2~0.2)		PC
(2.5~0.25)		PC
(2.5~0.2)
Indian Pines0.9120.9120.9050.906
Pavia U0.8560.8810.8580.883
Salinas0.9530.9530.9540.953

新窗口打开| 下载CSV


图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   Indian Pines,Pavia U和Salinas数据集分类结果图

Fig.10   Classification results of Indian Pines, Pavia U and Salinas data sets


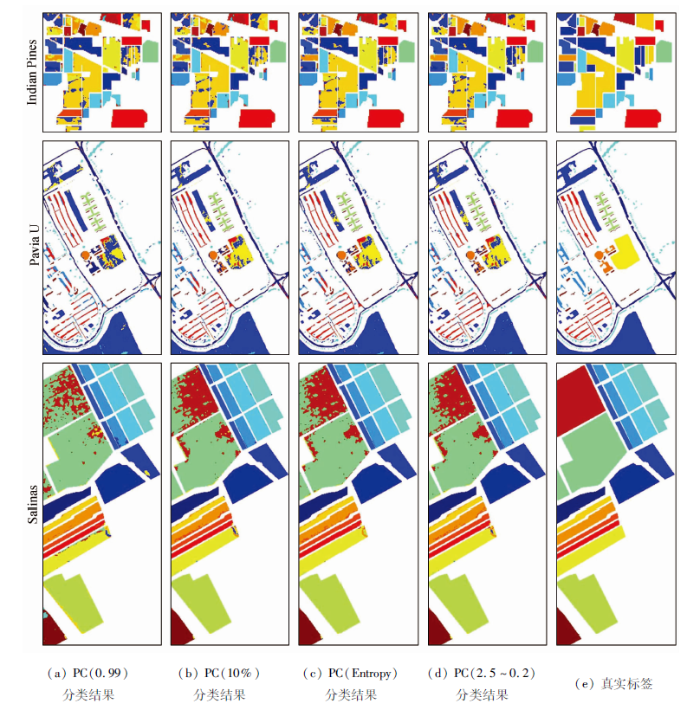
2.2.5 效果评价

为了进一步验证提出的方法的有效性,采用了2种使用较为广泛的传统方法和一种创新方法进行对比研究。第一种是利用累积方差贡献率进行主成分筛选,实验中阈值定为0.99(表示为PC(0.99))[11]; 第二种是Rodarmel等[21]提出的可以用5%~10%的主成分个数进行分类研究,实验中采用分类效果较好的10%(表示为PC(10%)); 第三种是Ibarrola-Ulzurrun等[22]创新提出的反映纹理特征指标即信息熵,选择大于信息熵标准差的主成分进行分类(表示为PC(Entropy))。

各主成分选择方法分类精度统计结果见表3,分类结果图见图11。对于Indian Pines和Salinas数据集,利用PC(2.5~0.2)分类的结果优于其他方法。对于Pavia U数据集,利用PC(2.5~0.2)分类的结果明显优于PC(0.99),且与PC(10%)、PC(Entropy)2种方法的分类精度差别不大。

表3   不同方法Kappa系数

Tab.3  Kappa coefficient of different methods

数据集PC
(0.99)		PC
(10%)		PC
(Entropy)		PC
(2.5~0.2)
Indian Pines0.8640.8530.8990.906
Pavia U0.7180.8840.8840.883
Salinas0.9100.9520.9510.953

新窗口打开| 下载CSV


图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   Indian Pines,Pavia U和Salinas数据集分类结果图

Fig.11   Classification results of Indian Pines, Pavia U and Salinas data sets


表4为Indian Pines数据集各地类的制图精度统计结果,数据为百分比。从表4可知,本文方法对于林地、大豆略耕地、燕麦地、牧草已割地、牧草地、玉米地、玉米未耕地和玉米略耕地的分类精度优于其他方法。同时,本文方法筛选出的主成分对于数量较少的地物较为敏感,塔楼、小麦地、燕麦地、牧草已割地、玉米地、苜蓿地、玉米地等分类效果明显优于其他方法。表5为Pavia U数据集各地类的制图精度统计结果,数据为百分比。从表5可知,本文方法对于裸地、柏油房顶、树的分类精度优于其他方法。同时,本文方法筛选出的主成分对于数量较少的树较为敏感,分类效果优于其他方法。表6为Salinas数据集各地类的制图精度统计结果,数据为百分比。从表6可知,该数据集各地类总体分类精度比较高,本文方法对于未培育的葡萄园、长叶莴苣的分类精度优于其他方法。同时,本文方法筛选出的主成分对于类别较少的长叶莴苣_6wk地物较为敏感,分类效果优于其他方法。表7为不同方法所选择的主成分个数。从表7可知,利用累计方差贡献率大于0.99选择的主成分个数因数据不同差别比较大,直接影响分类效果,不能作为一种适用于所有遥感影像数据的方法。利用10%的主成分个数的主成分开展分类效果可以,但无法解释其物理意义,且结果受波段总数影响较大,结果具有随机性。利用信息熵选择的主成分个数因数据不同差别比较大,当地物易分类时,所选择的主成分个数过多。利用信息熵进行主成分选择会选择出无信息的个别主成分,例如Indian Pines数据集的第49主成分,从图9来看,该主成分无明显的图像信息。本文方法受数据影响较小,均能筛选出数量适中的主成分。本文方法不仅可以剔除一些编号虽然较小,但是图像质量比较差的主成分,而且可以将编号较大,但是图像质量较好的图像参与运算。

表4   Indian Pines数据集制图精度

Tab.4  Prod. Acc of Indian Pines data set

地物种类PC
(0.99)		PC
(10%)		PC
(Entropy)		PC
(2.5~0.2)
塔楼100100100100
建筑物74.0275.281.4579.53
林地98.8998.8999.4399.51
小麦地100100100100
大豆地84.4679.7798.497.95
大豆略耕地86.7885.5690.8292.7
大豆未耕地89.489.1888.2686.98
燕麦地77.7877.786088.89
干草地100100100100
牧草已割地81.8290.9194.12100
草树地10099.77100100
牧草地10099.24100100
苜蓿地85.718086.8485.71
玉米地95.9593.9296.9597.97
玉米未耕地73.3273.0880.3982.93
玉米略耕地62.1457.9665.4465.54

新窗口打开| 下载CSV


表5   Pavia U数据集制图精度

Tab.5  Prod. Acc of Pavia U data set

地物种类PC
(0.99)		PC
(10%)		PC
(Entropy)		PC
(2.5~0.2)
草地95.394.7294.7293.54
砂砾42.8772.6372.6372.00
金属板10099.9199.9199.82
裸地31.5179.6479.6481.02
柏油房顶37.8467.8667.8674.26
阴影10010010099.83
砖块88.7894.3194.3193.75
树94.5895.1895.1895.41
沥青路面94.4597.0797.0796.44

新窗口打开| 下载CSV


表6   Salinas数据集制图精度

Tab.6  Prod. Acc of Salinas data set

地物种类PC
(0.99)		PC
(10%)		PC
(Entropy)		PC
(2.5~0.2)
葡萄园垂直架子98.2399.9299.8499.83
未培育的葡萄园146.8374.372.7275.26
长叶莴苣_7wk98.6699.8199.0499.81
长叶莴苣_6wk98.9599.4899.1299.48
长叶莴苣_5wk10010099.89100
长叶莴苣_4wk100100100100
衰败的绿色杂草99.35100100100
生长中的葡萄园100100100100
未培育的葡萄园294.2194.6294.6294.77
芹菜100100100100
作物残留100100100100
平整的休耕地99.83100100100
粗糙的休耕地100100100100
休耕地100100100100
椰菜299.95100100100
椰菜199.4999.91100100

新窗口打开| 下载CSV


表7   不同数据集筛选出的主成分信息

Tab.7  Principal component information selected by different data sets

数据集不同方法筛选的主成分编号个数
Indian PinesPC(0.99)1~2525
PC(10%)1~2020
PC(Entropy)1~46,4947
PC(2.5~0.2)1~8,10~25,28,29,38,59,66,68,88,92,101,10334
Pavia UPC(0.99)1~44
PC(10%)1-1010
PC(Entropy)1-1010
PC(2.5~0.2)1~10,16,19,23,24,43,7116
SalinasPC(0.99)1~33
PC(10%)1~2020
PC(Entropy)1~100100
PC(2.5~0.2)1~10,12,15~23,25,28,29,34,42,61,66,75,77,118,126,13432

新窗口打开| 下载CSV


3 结论

本文提出一种基于空间统计学的PCA变换后主成分选择的新方法,利用半变异函数参数变程、拱高/基台值的特性进行PCA变换后主成分的选择,取得了理想的效果,得出如下结论:

1)仿真实验证明了变程、拱高/基台值可以有效表达高光谱遥感影像空间相关性的范围和强弱。

2)变程、拱高/基台值的结果具有明显的互补性,联合两组参数可以有效剔除无意义主成分。

3)对比变程2~2.5和拱高/基台值0.2~0.25的不同参数组合的分类结果,变程2.5、拱高/基台值0.2的参数组合可以更加有效地筛选主成分。

4)和传统方法相比,本文提出的方法可以剔除主成分编号较小,但是图像质量较差的主成分,同时,筛选出主成分编号较大,但是图像质量较好的主成分。

5)在基于分类的研究中,利用变程2.5、拱高/基台值0.2进行PCA变换后主成分选择,不仅能够达到降维的目的,同时能够保证足够高的分类精度。和传统方法相比,本文方法可以更好地识别数量比较少的地类。

由于半变异函数参数的计算也是一个研究比较多的问题,确定更加准确的半变异函数参数会对主成分的选择产生一定的影响。除此之外,本文方法仅对PCA变换后的主成分选择进行了探讨,同时可以推广到最大噪声分数变换、独立成分分析等降维方法中去。

参考文献

Hughes G.

On the mean accuracy of statistical pattern recognizers

[J]. IEEE Transactions on Information Theory, 1968, 14(1):55-63.

DOI:10.1109/TIT.1968.1054102      URL     [本文引用: 1]

Chang C-I.

Hyperspectral Data Exploitation:Theory and Applications

[M]. John Wiley & Sons Inc,Hoboken,New Jersey, 2007,205.

[本文引用: 1]

宋海峰, 陈广胜, 杨巍巍.

基于PCA的高光谱遥感图像分类

[J]. 测绘工程, 2017, 26(12):17-20,26.

[本文引用: 1]

Song H F, Chen G S, Yang W W.

Principal component analysis for hyper spectral image classification

[J]. Engineering of Surveying and Mapping, 2017, 26(12):17-20,26.

[本文引用: 1]

Jolliffe I T.

Principal Component Analysis

[M]. Wiley, 2nd edition, 2002.

[本文引用: 1]

Pu R, Gong P, Tian Y, et al.

Invasive species change detection using artificial neural networks and CASI hyperspectral imagery

[J]. Environmental Monitoring and Assessment, 2008, 140(1-3):15-32.

DOI:10.1007/s10661-007-9843-7      URL     [本文引用: 1]

Chen G, Qian S.

Denoising and dimensionality reduction of hyperspectral imagery using wavelet packets,neighbour shrinking and principal component analysis

[J]. International Journal of Remote Sensing, 2009, 30(18):4889-4895.

DOI:10.1080/01431160802653724      URL     [本文引用: 1]

Canty M J, Nielsen A A.

Linear and kernel methods for multivariate change detection

[J]. Computers & Geosciences, 2012, 38(1):107-114.

DOI:10.1016/j.cageo.2011.05.012      URL     [本文引用: 1]

Foca G, Ferrari C, Ulrici A, et al.

The potential of spectral and hyperspectral-imaging techniques for bacterial detection in food:A case study on lactic acid bacteria

[J]. Talanta, 2016, 2016(153):111-119.

[本文引用: 1]

Li B, Hou B, Zhang D, et al.

Pears characteristics (soluble solids content and firmness prediction,varieties) testing methods based on visible-near infrared hyperspectral imaging

[J]. Optik International Journal for Light and Electron Optics, 2016, 127(5):2624-2630.

DOI:10.1016/j.ijleo.2015.11.193      URL     [本文引用: 1]

韩彦岭, 崔鹏霞, 杨树瑚, 等.

基于残差网络特征融合的高光谱图像分类

[J]. 国土资源遥感, 2021, 33(2):11-19.doi: 10.6046/gtzyyg.2020209.

[本文引用: 1]

Han Y L, Gui P X, Yang S H, et al.

Classification of hyperspectral image based on feature fusion of residual network

[J]. Remote Sensing for Land and Resources, 2021, 33(2):11-19.doi: 10.6046/gtzyyg.2020209.

[本文引用: 1]

Chang Y, Wang Y, Liu T, et al.

Fault diagnosis of a mine hoist using PCA and SVM techniques

[J]. Journal of China University of Mining and Technology, 2008, 18(3):327-331.

DOI:10.1016/S1006-1266(08)60069-3      URL     [本文引用: 2]

Li C, Liu L, Lei Y, et al.

Clustering for HSI hyperspectral image with weighted PCA and ICA

[J]. Journal of Intelligent & Fuzzy Systems:Applications in Engineering and Technology, 2017, 32(5):3729-3737.

[本文引用: 1]

臧卓, 林辉, 杨敏华.

利用PCA算法进行乔木树种高光谱数据降维与分类

[J]. 测绘科学, 2014, 188(2):146-149.

[本文引用: 1]

Zang Z, Lin H, Yang M H.

Dimension reduction and classification of hyperspectral data of tree species using PCA algorithm

[J]. Science of Surveying and Mapping, 2014, 188(2):146-149.

[本文引用: 1]

黄鸿, 曲焕鹏.

基于半监督稀疏鉴别嵌入的高光谱遥感影像分类

[J]. 光学精密工程, 2014, 22(2):434-442.

[本文引用: 1]

Huang H, Qu H P.

Hyperspectral remote sensing image classification based on SSDE

[J]. Optics and Precision Engineering, 2014, 22(2):434-442.

DOI:10.3788/OPE.20142202.0434      URL     [本文引用: 1]

Lee C, Youn S, Jeong T, et al.

Hybrid compression of hyperspectral images based on PCA with pre-encoding discriminant information

[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(7):1491-1495.

DOI:10.1109/LGRS.2015.2409897      URL     [本文引用: 1]

袁林, 胡少兴, 张爱武, 等.

基于深度学习的高光谱图像分类方法

[J]. 人工智能与机器人研究, 2017, 6(1):31-39.

[本文引用: 1]

Yuan L, Hu S X, Zhang A W, et al.

A classification method for hyperspectral imagery based on deep learning

[J]. Artificial Intelligence and Robotics Research, 2017, 6(1):31-39.

DOI:10.12677/AIRR.2017.61005      URL     [本文引用: 1]

臧卓, 林辉, 杨敏华.

ICA与PCA在高光谱数据降维分类中的对比研究

[J]. 中南林业科技大学学报, 2011, 31(11):18-22.

[本文引用: 1]

Zang Z, Lin H, Yang M H.

Comparative study on descending dimension classification of hyperspectral data between ICA algorithm and PCA algorithm

[J]. Journal of Central South University of Forestry & Technology, 2011, 31(11):18-22.

[本文引用: 1]

叶珍, 何明一.

PCA与移动窗小波变换的高光谱决策融合分类

[J]. 中国图象图形学报, 2015, 20(1):132-139.

[本文引用: 1]

Ye Z, He M Y.

PCA and windowed wavelet transform for hyperspectral decision fusion classification

[J]. Journal of Image and Graphics, 2015, 20(1):132-139.

[本文引用: 1]

Abdolmaleki M, Fathianpour N, Tabaei M.

Evaluating the performance of the wavelet transform in extracting spectral alteration features from hyperspectral images

[J]. International Journal of Remote Sensing, 2018, 2018:1-19.

[本文引用: 1]

Mather P, Koch M.

Computer processing of remotely-sensed images

[M]. John Wiley & Sons,Ltd, 2011,265.

[本文引用: 1]

Rodarmel C, Shan J.

Principal component analysis for hyperspectral image classification

[J]. Surveying and Land Information Systems, 2002, 62(2):115-122.

[本文引用: 2]

Ibarrola-Ulzurrun E, Marcello J, Gonzalo-Martin C.

Assessment of component selection strategies in hyperspectral imagery

[J]. Entropy, 2017, 19:1-17.

DOI:10.3390/e19010001      URL     [本文引用: 2]

Stephan K, Hibbitts C, Hoffmann H, et al.

Reduction of instrument-dependent noise in hyperspectral image data using the principal component analysis:Applications to Galileo NIMS data

[J]. Planetary and Space Science, 2008, 56(3-4):406-419.

DOI:10.1016/j.pss.2007.11.021      URL     [本文引用: 1]

Zheng W, Lai J, Yuen P.

GA-Fisher:A new LDA-based face recognition algorithm with selection of principal components

[J]. IEEE Transactions on Systems,Man and Cybernetics,Part B (Cybernetics), 2005, 35(5):1065-1078.

DOI:10.1109/TSMCB.2005.850175      URL     [本文引用: 1]

Zhang X, Li R, Jiao L.

Feature extraction combining PCA and immune clonal selection for hyperspectral remote sensing image classification

[C]. International Conference on Artificial Intelligence & Computational Intelligence,IEEE, 2009.

[本文引用: 1]

Tobler W.

Cellular geography

[M]. Springer Netherlands, 1979,379-386.

[本文引用: 1]

戴平生, 陈建宝.

空间统计学研究应用综述

[C]// 烟台: 国际应用统计学术研讨会, 2008.

[本文引用: 1]

Dai P S, Chen J B.

Review of spatial statistics research applications

[C]// Yantai: International Symposium on Applied Statistics, 2008.

[本文引用: 1]

Liu Q, Sun J, Chen Y, et al.

Spatial variability of soil heavy metals at different sampling scales

[J]. Chinese Journal of Soil Science, 2009, 40(6):1406-1410.

[本文引用: 1]

刘昌振, 舒红, 张志, 等.

基于多尺度分割的高分遥感图像变异函数纹理提取和分类

[J]. 国土资源遥感, 2015, 27(4):47-53.doi: 10.6046/gtzyyg.2015.04.08.

[本文引用: 1]

Liu C Z, Shu H, Zhang Z, et a1.

Variogram texture extraction and classification of high resolution remote sensing images based on multi-resolution segmentation

[J]. Remote Sensing for Land and Resources, 2015, 27(4):47-53.doi: 10.6046/gtzyyg.2015.04.08.

[本文引用: 1]

张亮.

基于PCA和SVM的高光谱遥感图像分类研究

[J]. 光学技术, 2008, 34(s1):184-187.

[本文引用: 1]

Zhang L.

Study on the hyperspectral remote sensed image classify based on PCA and SVM

[J]. Optical Technique, 2008, 34(s1):184-187.

[本文引用: 1]

王华, 李卫卫, 李志刚, 等.

基于多尺度超像素的高光谱图像分类研究

[J]. 自然资源遥感, 2021, 33(3):63-71.doi: 10.6046/zrzyyg.2020344.

[本文引用: 1]

Wang H, Li W W, Li Z G, et al.

Hyperspectral image classification based on multiscale superpixels

[J]. Remote Sensing for Natural Resources 2021, 33(3):63-71.doi: 10.6046/zrzyyg.2020344.

[本文引用: 1]

Goovaerts P. Geostatistics for natural resources evaluation[M]. NewYork City: Oxford University Press, 1997,266.

[本文引用: 1]

Cressie N.

Fitting variogram models by weighted least squares

[J]. Mathematical Geology, 1985, 17(5):563-586.

[本文引用: 1]

矫希国, 刘超.

变差函数的参数模拟

[J]. 物探化探计算技术, 1996, 18(2):157-161.

[本文引用: 1]

Jiao X G, Liu C.

Estimation of variation parameter

[J]. Computing Techniques for Geophysical and Geochemical Exploration, 1996, 18(2):157-161.

[本文引用: 1]

/

〈 〉

京ICP备05055290号-2
版权所有 © 2015 《自然资源遥感》编辑部
地址:北京学院路31号中国国土资源航空物探遥感中心 邮编：100083
电话:010-62060291/62060292 E-mail:zrzyyg@163.com
本系统由北京玛格泰克科技发展有限公司设计开发