0 引言
传统遥感图像全色锐化方法中,主要分为多分辨率分析方法和成分替代方法2类[5]。多分辨率分析方法的基本思想是多分辨率的分解与重构,通常通过线性分解的方法,从全色图像中提取空间细节信息,之后将其注入到多/高光谱图像中,使空间和光谱特征的渲染达到良好的平衡[5]。广泛使用的多分辨率分析方法包括拉普拉斯金字塔分解[6]、多孔小波变换(à trous wavelet transform, ATWT)[7]、形态算子融合(morphological operators fusion, MOF)法[5]、高通滤波(high pass filtering, HPF)[8]、基于平滑滤波器的强度调制(smoothing filter-based intensity, SFIM)[9]等。成分替代方法首先将多光谱图像的空间结构和光谱信息分离,然后将原始图像的空间信息成分替换为高空间分辨率图像。经典的基于成分替代的融合方法包括强度-色调-饱和度(intensity-hue-saturation, IHS)融合方法[10]、主成分分析(principal component analysis, PCA)融合方法[11]、Gram-Schmidt(GS)变换融合方法[12]、色彩标准化变换(Brovey)融合方法[4]、基于物理约束的波段相关空间细节方法(band-dependent spatial detail with physical constrains, BDSD-PC)[4]等。成分替代法可以得到丰富的空间信息,但通常伴随着光谱失真较为严重的问题。此外,还有学者利用深度学习的方法来探索源图像的层次特征以解决全色锐化问题。常见的基于深度学习的全色锐化方法有卷积神经网络(convolutional neural network, CNN)、深度残差全色锐化神经网络(deep residual pan-sharpening neural network,DRPNN)等[13]。
对于高光谱图像空间分辨率上的提升虽然己有很多成果,但是融合的结果仍然会出现光谱失真、图像视觉效果不佳等情况[14]。原因主要有2个方面: 一方面,传统全色锐化方法往往没有考虑高分遥感图像中的区域像素差异,仅仅在固定的矩形窗口中注入分割信息,忽略像素间的相关性,容易造成融合图像严重的光谱和细节失真; 另一方面,高光谱图像的波段数目多,需要考虑与多光谱波段的对应,波段匹配的准则也会影响融合结果。交叉皮层模型(intersecting cortical model, ICM)是基于脉冲耦合神经网络模型(pulse coupled neural network, PCNN)改进的单层神经网络模型,与PCNN相比参数较少,且保留了PCNN变阈值、同步脉冲发放的特性,也不需要进行训练[15]。其独特的生物学背景还能够突出图像的细节部分,同时保留图像轮廓部分,目前被广泛应用于图像处理领域。传统方法通常将ICM参数和迭代次数都设为固定的值,需要多次测试激活条件才能找到最佳参数,严重影响图像的融合效果。
为解决ICM参数选取不易的问题,以及利用分割的非规则区域进行自适应细节注入,获得细节和光谱保留更好的高光谱图像,本文提出一种基于ICM神经元模型的自适应高光谱图像全色锐化算法。首先将高光谱与多光谱图像进行波段匹配融合,生成中分辨率高光谱图像; 再自适应注入全色图像的空间细节。利用灰狼优化算法(grey wolf optimizer, GWO)优秀的全局搜索能力,将优化的ICM模型用于高光谱遥感图像的分割,用分割得到的非规则区域计算空间细节注入的增益权重。与其他几种经典融合方法的对比实验表明,本方法在较好实现光谱保持的同时,增加了空间纹理细节,获得兼具高空间分辨率和光谱分辨率的高光谱图像。
1 理论基础
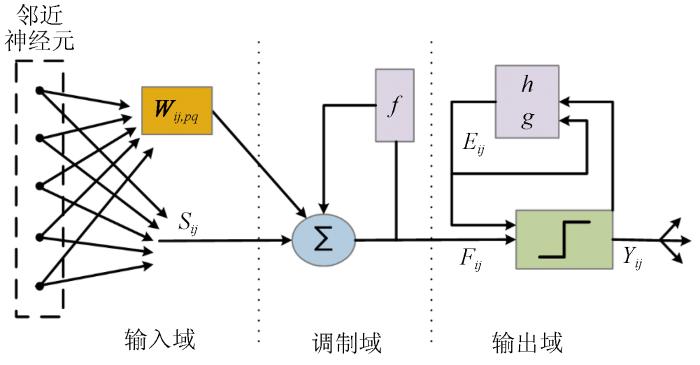
1.1 交叉皮层神经元模型
图1
式中: 索引i,j和索引p,q分别为当前神经元位置和邻域神经元位置; p,q为与i,j神经元相连接的八邻域神经元; Ns(ij)为神经元i和j的八邻域; n为迭代次数; OP为邻域神经元输入,由邻近神经元脉冲输出Ypq和权值矩阵Wijpq组成; Sij为外部活动刺激,即输入的遥感图像灰度值; Fij为反馈输入; Eij为活动阈值; f和g分别为Fij和Eij的衰减系数; 系数h决定神经元在被激发后阈值的增量; 在模型运行中,当Fij>Eij时,模型中的神经元被激发,产生输出脉冲,神经元发生点火,此时阈值Eij大幅增加,并随着迭代进行在衰减因子g的作用下不断衰减,当衰减到小于内部活动项时,神经元再次点火,如此迭代循环。
1.2 GWO算法
GWO算法是一种群体智能优化方法,通过模拟灰狼群体协作捕食的过程实现优化的目的[18]。首先定义狼群中最佳的前3只领头狼依次为α,β和δ,它们领导其他狼朝向搜索空间中有希望的区域。其余的灰狼定义为搜索狼ω,它们环绕α,β或δ进行比较,等待位置更新。算法具体实施步骤如下:
1)初始化灰狼种群,随机产生n个狼的位置; 初始化收敛因子a、系数矩阵A和C的值; 初始化领头狼α,β,δ的位置Xα,Xβ,Xδ的值。
2)计算每只狼的适应度值。
3)比较第i只搜索狼的适应度值fi和Xα,Xβ及Xδ的适应度值,若fi更优,则用Xi更新Xα,Xβ或Xδ。
4)所有狼根据式(5)—(7)活动,并按照式(8)—(10)计算a,A和C的值,直至每只搜索狼的位置都得到更新。式中: t为当前迭代; T为最大迭代次数; X(t)为当前搜索狼的位置向量; X(t+1)为更新后的搜索狼的位置向量; r1和r2为[0,1]之间的随机数。α,β,δ狼与其他灰狼个体的距离为:
搜素狼向α,β,δ狼移动,公式为:
搜素狼的最终位置,公式为:
系数计算公式为:
5)根据适应度条件,如果达到结束条件,则迭代结束; 否则返回2)。
2 基于参数自适应ICM的全色锐化算法
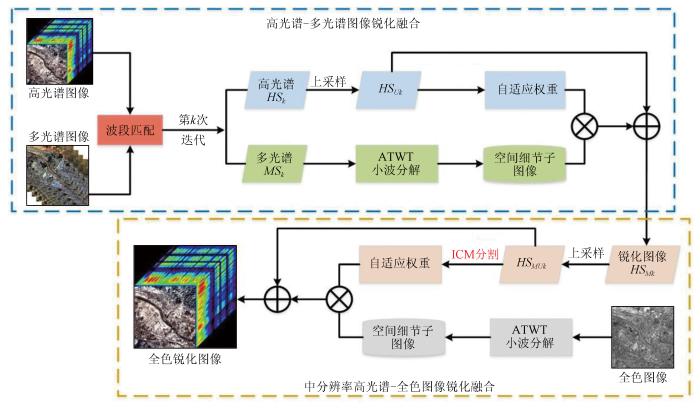
由于高光谱图像与全色图像的空谱分辨率差异较大,且高光谱图像光谱波段众多,数据存在冗余,直接利用全色图像实现高光谱图像的全色锐化容易导致严重的空谱失真。然而多光谱图像的空谱分辨率介于两者之间,在融合中可以为高光谱图像提供空间信息。考虑到图像各自的特点,本文提出将高光谱图像先与多光谱图像进行锐化融合,得到的中分辨率高光谱图像再与全色图像进行融合的思路,完成高光谱图像全色锐化。本文算法流程如图2所示,主要包括波段匹配、参数自适应ICM设计、高光谱-多光谱图像锐化融合和中分高光谱-全色图像锐化融合几个部分,图中表示自适应权重与提取的空间细节子图像点积,得到注入增益; 表示将注入增益与上采样的高光谱图像对应相加。
图2
2.1 波段匹配
在高光谱与多光谱图像的锐化过程中,由于波段数量上属于“多对多”融合,因此波段的对应性是必须要考虑的关键问题[14]。通过制定准则,选择包含最相关信息的多光谱波段来增强当前高光谱波段,使产生的光谱失真最小,也是减少多通道图像冗余的一种有效方法。本文采用融合评价指标空间相关系数(spatial correlation coefficient, SCC)值为准则,匹配高光谱和多光谱图像的波段。具体方法为将多光谱的m个波段分别与h个高光谱波段计算SCC值,得到m×h数据矩阵。每个高光谱波段的m个SCC值中,最大值所在波段,即为该高光谱波段匹配的多光谱波段。SCC的数学表达式为:
式中: $H S_{(i, j)}$和$M S_{(i, j)}$分别为高光谱图像和多光谱图像在i,j位置上的像素值; μHS和μMS分别为高光谱图像和多光谱图像的均值。
同时,若匹配的每组波段对中高光谱波段数大于5,则使用最优聚类框架(optimal clustering framework, OCF)[19]进行高光谱波段选择,波段选择的数量设置为5; 若高光谱波段数小于等于5,则保持原有波段,从而减少高光谱图像信息冗余导致的细节注入增益权重计算误差。
2.2 参数自适应ICM设计
当ICM应用于图像分割时,参数f和g的选择尤为重要,二者共同影响着图像像素的激活状态。但在传统的ICM模型中,往往使用固定不变的经验值,并且每换一幅图像都需人工再重新设置参数,确定最终参数的过程复杂且不稳定。本研究采用灰狼优化算法优化ICM模型参数,实现参数的配置自适应,在迭代中获得参数f和g的组合最优解。
本文方法中,设每只狼的位置X为参数f或g值的一个值,搜索食物的过程,即为寻找ICM参数最优配置的过程。本文利用空间相关系数SCC和光谱角映射(spectral angle mapper, SAM)构建适应度函数,适应度函数fitness公式为:
式中: M为图像中的像素个数; HS和HSO分别为原始高光谱图像和全色锐化图像。SCC和SAM的结合能够从空间和光谱质量2个方面综合评价图像。参数f和g的值在搜索狼位置的迭代更新中,不断提高自己的适应度,直到满足迭代终止条件即融合指标最佳。
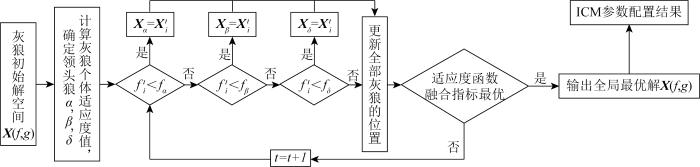
本文通过将GWO与ICM相结合,利用ICM模型的脉冲发放特性和GWO的空间随机搜索能力,来求解ICM中2个参数的最优值,解决了ICM参数需要人工设置的问题,实现了ICM分割参数的自适应。结合GWO的ICM参数优化流程如图3所示。
图3
2.3 高光谱与多光谱图像锐化融合
高光谱与多光谱图像锐化融合步骤如下:
1)将原始高光谱遥感图像HS的h个波段和原始多光谱图像MS的m个波段进行配,得到h组波段对。
2)在已匹配的每组波段对中,对HS按照MS大小,利用双三次非线性插值进行上采样得到HSU。
3)波段选择,使每组波段对中HS波段数小于等于5,得到HSC。
4)对MS执行ATWT小波分解,分解出高频和低频细节,将高频细节置0后,再执行小波逆变换得到图像MSL,计算MS的空间细节DMS,公式为:
5)实现自适应ICM模型,将归一化的像素值Sij作为外部输入,对波段选择后的HSC图像第k波段进行自适应参数ICM分割。用得到的非规则区域计算图像特征,并计算增益权重
式中: Cov()为协方差; Std()为标准差。
6)将MS的空间细节按照增益权重注入到HSU中,得到中分高光谱图像HSMk,计算融合结果,具体计算公式为:
2.4 中分辨率高光谱与全色图像锐化融合
中分辨率高光谱与全色图像锐化融合步骤为:
1)对得到的中分辨率高光谱图像HSM进行双三次非线性插值上采样,得到分辨率为原始全色图像PAN大小的高光谱图像HSMU。
2)对PAN执行ATWT小波分解,分解出高频和低频细节,将高频细节置零后,再执行小波逆变换得到图像PANL。计算出全色图像细节DPAN,公式为:
3)实现自适应ICM模型,将归一化的像素值Sij作为外部输入,对HSM第k波段进行自适应参数ICM分割。用得到非规则区域计算图像特征,并计算增益权重
4)计算最后的融合图像HSOk。具体公式为:
3 实验结果与分析评价
3.1 实验数据集
为验证本文所提出算法的有效性,采用刘家峡山地区域和兰州市城市区域2个数据集进行了验证实验,其中高光谱图像来自资源一号02D遥感卫星,多光谱图像和全色图像来自高分二号遥感卫星。高光谱图像包含166个波段,分辨率36 m,尺寸为108像素×108像素; 多光谱图像包含蓝光、绿光、红光、近红外4个波段,分辨率4 m,尺寸为972像素×972像素。全色图像空间分辨率1 m,尺寸为3 888像素×3 888像素。由于源图像来自不同卫星获取的数据,因此在融合之前,已对所有图像进行配准预处理。
3.2 锐化质量评价指标
RMSE可以测量全色锐化图像和参考图像的差异程度,其值越接近0,表示融合质量越好; PSNR用于评估图像空间信息重构的丰歉程度,2幅图像间的PSNR值越大,则越相似; ERGAS能够客观地反映融合图像整体质量,其值由RMSE的总和组成,越接近0表示2幅图像相似度越高; SSIM指标从亮度、对比度和结构3个方面衡量2幅图像的相似性,在图像质量评价中更符合人眼视觉特性,理想值为1; DD能够直接反映图像的光谱扭曲程度,以2幅图像灰度平均值的差值计算光谱变化程度,DD值越大说明光谱扭曲越严重,理想值为0; SAM用于测量图像的全局光谱失真度,SAM值越低表示光谱失真越少,理想值为0。
3.3 对比实验
为了验证本文算法锐化融合结果的有效性,将本文方法分别与GS[12], PCA[11], Brovey[4], IHS[10], ATWT[7], HPF[8], SFIM[9], BDSD-PC[4]这8种方法进行了对比。其中GS, PCA, Brovey, IHS, BDSD-PC方法属于成分替代方法; ATWT, HPF, SFIM方法属于多分辨率分析方法。图4和图5分别为刘家峡山地数据集和兰州城市数据集不同融合方法的对比结果。其中图4(a)和图5(a)为原始高光谱遥感图像,图4(b)和图5(b)是采用本文方法的融合结果,图4(c)—(j)、图5(c)—(j)是不同对比方法的融合结果图像。图4刘家峡山地数据集中,山地内植被丰富。从图中可以看出,GS, PCA, Brovey, IHS这4种成分替代方法相较于多分辨率分析方法明显出现了较大的光谱扭曲,整体色调发生变化。成分替代方法之所以在光谱保留这方面有很大的劣势,是由于它基于图像全局的融合方式,全色图像和多、高光谱图像之间局部差异的情况没有被充分考虑,而该差异是由全色图像和多、高光谱图像波段之间的光谱不匹配引起的,就会导致明显的光谱失真。以PCA方法为例,该方法使用全色图像替换第一主成分分量,但由于变换后的第一主成分中也含有部分光谱信息,故可能存在着严重的光谱失真。本文方法融合结果的光谱特征与原始高光谱图像最为接近,光谱扭曲最小,能够较好地保持光谱信息,验证了所提算法对于光谱保真方面的性能。同时,从图中可以看出,本文方法对于空间纹理细节的注入较为全面。因此,本文提出的结合ICM自适应全色锐化算法在光谱保真和空间丰富的主观定性评价中效果较好。
图4
图5
表1 刘家峡山地数据集全色锐化比较结果
Tab.1
| 方法 | RMSE | PSNR/dB | ERGAS | SSIM | DD | SAM/(°) |
|---|---|---|---|---|---|---|
| 本文方法 | 20.009 7 | 30.177 6 | 0.451 4 | 0.608 8 | 8.602 3 | 2.291 6 |
| GS | 32.571 1 | 21.565 7 | 0.815 6 | 0.577 1 | 26.195 0 | 2.433 0 |
| PCA | 32.249 5 | 21.650 8 | 0.810 0 | 0.579 5 | 25.912 7 | 2.413 0 |
| Brovey | 34.867 1 | 20.970 2 | 0.854 4 | 0.568 3 | 28.263 1 | 2.412 2 |
| IHS | 40.792 3 | 18.978 6 | 1.054 0 | 0.516 4 | 33.807 7 | 2.864 0 |
| ATWT | 22.164 7 | 24.803 8 | 0.626 4 | 0.587 3 | 17.033 3 | 2.635 9 |
| HPF | 23.479 3 | 24.319 2 | 0.652 9 | 0.569 7 | 18.144 1 | 2.293 1 |
| SFIM | 22.284 9 | 24.761 2 | 0.629 2 | 0.572 8 | 17.070 9 | 2.295 1 |
| BDSD-PC | 29.697 2 | 22.400 5 | 1.502 4 | 0.484 9 | 22.725 8 | 4.139 5 |
表2 兰州城市数据集全色锐化比较结果
Tab.2
| 方法 | RMSE | PSNR/dB | ERGAS | SSIM | DD | SAM/(°) |
|---|---|---|---|---|---|---|
| 本文方法 | 49.055 6 | 19.191 1 | 1.717 0 | 0.599 7 | 35.245 5 | 4.780 3 |
| GS | 65.213 0 | 16.764 2 | 1.880 6 | 0.459 9 | 52.089 3 | 4.972 8 |
| PCA | 64.608 2 | 16.845 4 | 1.875 0 | 0.462 5 | 51.600 5 | 4.948 4 |
| Brovey | 57.400 8 | 17.895 1 | 1.799 8 | 0.496 3 | 45.718 0 | 4.934 3 |
| IHS | 72.438 5 | 15.347 1 | 2.099 2 | 0.426 6 | 57.988 8 | 5.358 0 |
| ATWT | 55.754 9 | 18.100 8 | 1.793 8 | 0.472 8 | 44.263 7 | 5.280 2 |
| HPF | 57.058 7 | 17.903 9 | 1.807 8 | 0.465 9 | 45.314 7 | 4.901 8 |
| SFIM | 56.417 8 | 18.001 4 | 1.801 0 | 0.468 3 | 44.791 7 | 4.913 1 |
| BDSD-PC | 50.277 3 | 18.821 6 | 1.765 3 | 0.455 9 | 39.718 2 | 5.437 6 |
4 结论
高光谱图像为遥感应用提供了更加丰富的谱段信息,然而其较低的空间分辨率严重影响了高光谱图像的应用,通过全色锐化等遥感图像融合方法提升图像空间分辨率,可以大大提升其应用价值。
本文提出了一种自适应参数ICM高光谱图像全色锐化算法。该算法通过先将高光谱与多光谱图像的波段进行匹配,然后利用多分辨率分析方法进行对应融合,再将结果与全色图像融合的方法,获得了细节和光谱保留更好的高光谱图像。同时,本文算法利用GWO算法解决了ICM参数不易确定问题。通过资源一号02D的2组高光谱数据验证实验,证明了本文算法相较于其他算法,在融合结果的空间细节与光谱保持方面表现更好。
高光谱图像与全色图像的波段数量和空间分辨率差异较大,因此高光谱图像的全色锐化实现的挑战性也更大,进一步优化神经网络模型、开展高光谱图像自适应全色锐化算法将是团队下一步工作。
参考文献
基于超像素分割的RGB与高光谱图像融合
[J].
Fusion of RGB and hyperspectral images based on super-pixel segmentation
[J].
Fusing China GF-5 hyperspectral data with GF-1,GF-2 and Sentinel-2A multispectral data:Which methods should be used
[J].
高分五号高光谱数据融合方法比较
[J].
Comparison of fusion methods on GF-5 hyperspectral data
[J].
Robust band-dependent spatial-detail approaches for panchromatic sharpening
[J].
Fusion of multispectral and panchromatic images based on morphological operators
[J].
DOI:10.1109/TIP.2016.2556944
PMID:28113904
[本文引用: 3]

Nonlinear decomposition schemes constitute an alternative to classical approaches for facing the problem of data fusion. In this paper, we discuss the application of this methodology to a popular remote sensing application called pansharpening, which consists in the fusion of a low resolution multispectral image and a high-resolution panchromatic image. We design a complete pansharpening scheme based on the use of morphological half gradient operators and demonstrate the suitability of this algorithm through the comparison with the state-of-the-art approaches. Four data sets acquired by the Pleiades, Worldview-2, Ikonos, and Geoeye-1 satellites are employed for the performance assessment, testifying the effectiveness of the proposed approach in producing top-class images with a setting independent of the specific sensor.
A bayesian procedure for full-resolution quality assessment of pansharpened products
[J].
Contrast and error-based fusion schemes for multispectral image pansharpening
[J].
Multispectral and hyperspectral image fusion in remote sensing:A survey
[J].
Hyperspectral sharpening approaches using satellite multiplatform data
[J].
A new IHS and wavelet based pansharpening algorithm for high spatial resolution satellite imagery
[J].
A novel iterative PCA-based pansharpening method
[J].
DOI:10.1080/2150704X.2018.1547443
[本文引用: 2]

Image pansharpening methods are usually grouped into two main classes: the spectral methods and the spatial methods. For the first class, the multispectral image undergoes a spectral transformation and then one of the resultant components is totally substituted with the panchromatic image, hence leading to a considerable color distortion compared with the second class. In the literature, this issue is addressed by integrating the wavelet transform to the spectral methods in order to transfer only the spatial details of the panchromatic image. Furthermore, the spatial information quantity transferred during the fusion is usually defined by the resolution ratio between the multispectral and panchromatic images, and this is, however, not necessarily the optimal quantity providing the best images. Therefore, a simple iterative Principal Component Analysis (PCA) based method is proposed in this letter, to continuously transfer the spatial information from the panchromatic to the multispectral image until the best fused image is obtained. The spatial distortion D-s of the Quality with No Reference (QNR) index is used as a stopping criterion. The experiments applied on the Worldview-3 images show that the suggested method presents the best visual and numerical results comparatively to the PCA and the Additive Wavelet Principal Component (AWPC) methods.
Improving component substitution pansharpening through multivariate regression of MS + Pan data
[J].
基于深度学习的空谱遥感图像融合综述
[J].
A review of pansharpening based on deep learning
[J].
多源遥感图像融合发展现状与未来展望
[J].
Development status and future prospects of multi-source remote sensing image fusion
[J].
Feature linking via stimulus-evoked oscillations:Experimental results from cat visual cortex and functional implications from a network model
[C]//
基于PCNN图像分割的医学图像融合算法
[J].
Medical image fusion algorithm based on PCNN image segmentation
[J].
一种多光谱遥感影像与航拍影像融合算法
[J].
A fusion algorithm of multispectral remote sensing image and aerial image
[J].
双模狩猎的灰狼优化算法在多阈值图像分割中应用
[J].
Grey wolf optimization algorithm with double-hunting modes and its application to multi-threshold image segmentation
[J].
Optimal clustering framework for hyperspectral band selection
[J].
Fusing hyperspectral and multispectral images via coupled sparse tensor factorization
[J].
Fusion of hyperspectral and multispectral images:A novel framework based on generalization of pan-sharpening methods
[J].
Fusion of China ZY-1 02D hyperspectral data and multispectral data:Which methods should be used
[J].