0 引言
目前点云精简方法按照是否构建点云三角网分为直接采用点云和基于三角网格2种,基于三角网格的点云精简方法首先建立点云拓扑网格关系,然后合并细节较小的网格,去除对应点云,达到精简目的,主要包括包络网格法、顶点聚类法、区域合并法、边折叠法、小波分解等方法[5]。但存在建立点云拓扑结构速度慢的问题,且需按照一定阈值识别三角网以实现点云精简。直接采用点云的精简方法是根据空间位置关系计算出对应的离散几何信息实现精简[6],主要包括根据比例压缩、基于聚类压缩、基于曲率压缩、基于信息量压缩和基于网格等方法实现点云精简。葛源坤[7]针对平坦研究区采用包围盒法,针对突变区域采用基于点云曲率的最小距离法,结果表明将2种常用的点云精简方法结合可保证点云的关键几何信息; 陈西江等[8]首先利用主成分分析(principal component analysis,PCA)方法估计点云法向量及其夹角,然后利用最邻近点获取法向量夹角的信息熵,根据熵的大小实现点云精简; Han等[9]首先计算点云法向量,然后基于法向量识别和保留边缘点,删除非边缘点,实现点云精简; 苏本跃等[10]采用K-means对点云曲率进行聚类可以实现点云的去噪和精简处理; 唐林[11]提出保留点云属性的点云精简方法,即对所有的点云数据X-Y边界快速提取并保留,且对提取过边界的散乱点构建K邻域,通过邻域计算模糊熵和曲率,将曲率小于所设阈值的点剔除以实现点云精简。结合上述可知,实现点云精简方法是多样的,主要通过不同方法对点云的特征信息进行处理,以实现精简。其中K-means聚类方法可以实现点云精简处理,但仅对点云曲率进行聚类,对其他特征信息的聚类是否可实现聚类需进一步探讨。根据上述分析,本文在计算点云法向量的基础上,利用K-means++聚类方法对点云法向量聚类实现点云精简,并通过计算相关系数验证点云精简的有效性。
1 研究区概况及数据源
1.1 研究区概况
以新疆第八师一五零团五连周边荒漠(E85°58'35″~85°59'4″,N44°57'29″~44°58'0″)作为无人机LiDAR数据获取的研究区,该荒漠区整体高程变化小,主要以旱生和沙生灌木为主,如梭梭、骆驼蓬、麻黄、碱蓬草和驼绒藜等。
以Scout B1-100单旋翼油动无人直升机作为飞行平台,搭载Riegl VUX-1激光扫描仪系统、OxTS Survey+2惯性导航系统和可见光相机,于2017年7月31日在研究区正上方以60 m的航高、6 m/s的巡航速度,550 kHz的扫描频率采集数据。激光扫描仪的基本参数见表1。Survey+2系统定位精度可达2 cm,横滚和俯仰精度为0.03°。
表1 激光扫描仪Riegl VUX-1主要参数
Tab.1
| 扫描仪参数 | 规格 |
|---|---|
| 扫描速度/(转·s-1) | 10~200 |
| 最小测量距离/m | 5 |
| 激光脉冲频率/kHz | 550 |
| 测量精度/mm | 15 |
| 角度分辨率/(°) | 0.001 |
| 最大视场角/(°) | 330 |
| 回波强度/bit | 16 |
| 回波次数 | 无限 |
在获取研究区扫描仪、惯性导航数据和可见光数据后,使用Riegl 公司提供的配套软件对点云数据进行航带裁剪拼接、扫描仪数据姿态矫正、点云去噪声点的预处理。截取部分实验区域作为本文的研究区,且以WGS_1984_UTM_Zone_44 N为投影坐标系导出点云数据,以.las格式存储点云。
1.2 数据源
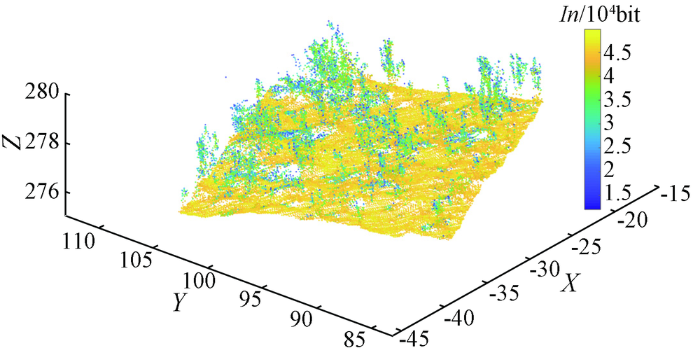
经统计,研究区点云总个数为69 544,令X,Y,Z,In,Re,An分别表示点云三维坐标、回波强度值、回波次数和扫描角度,则研究区X范围为[-46.065 0,-15.002 3],Y范围为[83.958 8,112.144 5],Z范围为[275.863 0,280.533 3],In范围为[12 036,49 850],激光扫描仪系统记录的最大Re为5,An范围为[41°,54°]。研究区点云以回波强度进行三维可视化的结果如图1所示。
图1
图1
研究区原始点云回波强度渲染结果
Fig.1
Visualization of the original point cloud echo intensity in study area
2 研究方法
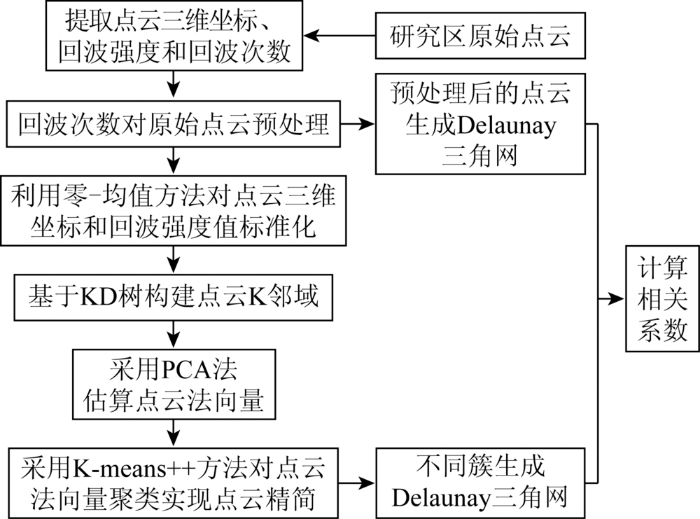
本研究技术流程如图2所示。
图2
采用MATLAB R2017a软件提取X,Y,Z,In和Re,对X,Y,Z和In进行标准化以减少量纲引起的误差。在利用KD树(K-dimension tree)实现散乱点云的结构存储基础上,构建点云的K邻域,且利用PCA法估算得到点云法向量[12]。利用Python编程实现肘方法以确定K-means++方法的最佳聚类数目,进而采用K-means++方法对法向量进行聚类。接着,三维可视化不同聚类结果,通过目视解译获取保存研究区地物特征较好的簇,对簇中点云生成Delaunay三角网,对比参与聚类前点云生成的Delaunay三角网,且将三角网转换为栅格数据计算它们的相关系数,分析点云精简结果。
2.1 基于回波次数的点云预处理
聚类方法原理是根据不同距离来度量数据相似性,因此为了消除数据量纲和取值范围差异的影响,需对数据进行标准化[15],本文采用零-均值标准化方法将数据变为标准正态分布,标准化方程为
式中: μt和σt分别为点云属性t的均值和标准差; ti表示第i点的属性,包括点云三维坐标X,Y,Z和强度In; N为点云个数; χt和χ't分别表示属性标准前后的数据。根据上述分析,仅需对第1次回波点云中的三维坐标和回波强度值进行标准化处理。
2.2 点云K邻域构建
2.3 点云法向量估算
式中: η为平面β的法向量; d为β到坐标原点的距离; K为点p最近K个点; argmin为当函数取最小值时对应自变量的取值;
2.4 K-means++聚类方法
2.4.1 K-means++聚类原理
通过K-means聚类可以较好地对点云进行精简[21],且K-means++聚类是对K-means聚类方法的改进,K-means++聚类通过使初始聚类中心点彼此尽可能远离的方法,使聚类结果更好、更一致,其初始聚类中心的选择步骤为:
1)初始化空数据集合M,存放k个聚类中心;
2)从输入数据中随机选择第一个中心点ci,将其加入集合M中;
3)对于集合M外的每一个样本点pi,计算pi到ci的距离D(pi),并找到D2(pi)最小的样本点p'i;
4)使用加权概率分布
5)重复步骤2)—4),至选定k个初始中心。
根据上述方法得到k个初始聚类中心ci,i=1,2,…,k。接着执行K-means算法,先设置最大迭代次数m和收敛的阈值ε。同时根据距离标准,计算每个样本点到中心ci之间的距离,且将该样本点划分到距离它最近的中心点ci,i∈1,2,…,k; 计算每个类别中相邻2次聚类中心变量D(pi),判断D(pi)是否小于收敛阈值ε,如果大于ε,且未达到最大迭代次数,则继续聚类; 否则终止聚类。
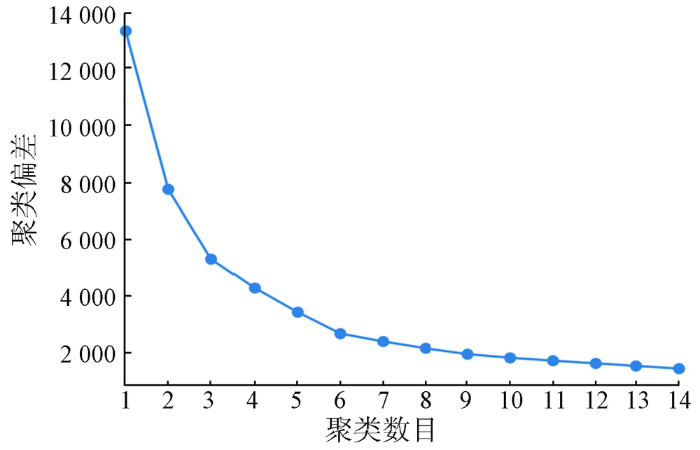
2.4.2 肘方法确定最佳聚类数目
式中: N为样本个数; k为聚类数目; pi为第i个样本点; cj为簇j的中心; 如果样本pi属于簇j,则w(i,j)=1,否则w(i,j)=0。
K-means聚类方法的另一个难点是初始聚类中心的选择。为了得到最优的聚类结果,本文在随机选择初始聚类中心和采用肘方法最佳聚类数目的基础上,针对不同的随机初始中心独立运行K-means聚类方法100次,接着从中选择SSE最小的作为最终模型。
2.5 点云精简验证
不规则三角网(triangulated irregular network,TIN)是点云的组织方式之一,其将点云按照一定区域的点云密度和位置划分为不规则的三角形网格。常见的TIN是Delaunay三角网,其满足最大最小角特性、最大空外接圆特性和唯一性[25]。最大最小角特性是指由点集形成的所有三角网中,Delaunay三角网中三角形的最小角度却是最大的。最大空外接圆特性是指由点集所形成的每一个三角形的外接圆均不包含点集中的其他任意点,即每个Delaunay三角网都是选择最近的点构建三角形。因为建立Delaunay三角网必须遵从以上2个特性,所以针对同一数据,不管采用什么建立三角网方法,其结果是唯一的。本文选择Delaunay三角网对点云进行重新组织可视化,且利用ArcGIS10.3软件将三角网转换为栅格数据,采用band collection statistics工具计算聚类前和聚类后对应栅格的相关系数。
3 结果与分析
3.1 点云法向量估算结果
3.1.1 点云K邻域构建
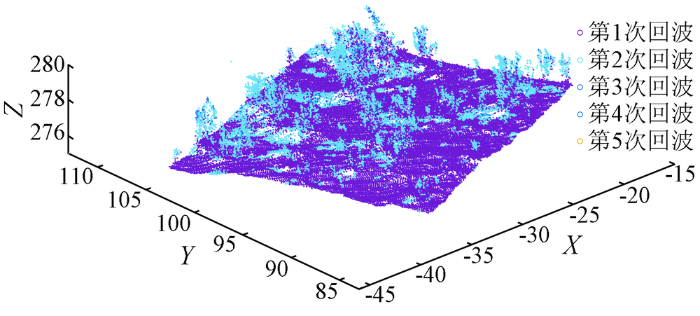
研究区原始点云回波次数三维可视化如图3,通过分析图可知,第1次回波点云个数为61 822,第2—5次回波分别对应的点云个数为7 359,354,7和2,且第1次回波对应的点云包含了研究区全部地物,所以可去除多次回波点云,只针对第1次回波点云进行K-means++聚类实现点云精简。针对第1次回波对应的61 822个点云构建每个点云的K邻域,以欧氏距离作为度量标准,为了验证本文方法可行性,选取K=10以构建点云的K邻域,即每个点的邻域是由与该点距离最近的10个点组成。借助Python中Scikit-learn库,实现基于KD树来构建点云K邻域。为详细说明构建邻域的过程,本文选择部分点云进行说明,表2是索引号为1,2,3对应的K邻域,如以点云索引为1为例,即索引号为1的K邻域是由点云索引号为45,1,44,46,142,141,461,222,346和462构成的,其他点云类似。
图3
图3
研究区原始点云回波次数三维可视化结果
Fig.3
3D visualization results of original point cloud echo times in study area
表2 部分点云K邻域对应的索引号
Tab.2
| 索引号 | K邻域点云对应的索引号 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 45 | 1 | 44 | 46 | 142 | 141 | 461 | 222 | 346 | 462 |
| 2 | 46 | 0 | 2 | 47 | 142 | 45 | 143 | 462 | 463 | 3 |
| 3 | 3 | 1 | 47 | 48 | 46 | 463 | 143 | 4 | 464 | 556 |
利用MATLAB软件编程找到每个点云邻域对应的三维坐标和回波强度值信息,表3是索引号为1对应K邻域的点云属性信息,其中Xstan,Ystan,Zstan和Instan分别为三维坐标和强度标准化后的数值。可以通过编程获取所有点云K邻域对应的属性信息,以实现点云K邻域的构建。
表3 索引号1对应的点云属性信息
Tab.3
| 索引号 | Xstan | Ystan | Zstan | Instan |
|---|---|---|---|---|
| 45 | -1.362 | -1.096 | 0.308 | 1.097 |
| 1 | -1.340 | -1.101 | 0.304 | 0.968 |
| 44 | -1.378 | -1.085 | 0.329 | 0.983 |
| 46 | -1.344 | -1.108 | 0.323 | 1.198 |
| 142 | -1.345 | -1.113 | 0.337 | 1.058 |
| 141 | -1.360 | -1.103 | 0.347 | 1.140 |
| 461 | -1.380 | -1.118 | 0.315 | 1.239 |
| 222 | -1.375 | -1.099 | 0.355 | 1.221 |
| 346 | -0.609 | -1.632 | 0.620 | 0.179 |
| 462 | -1.362 | -1.131 | 0.314 | 1.094 |
3.1.2 点云法向量估算结果
对点云邻域进行PCA分析,找到最小特征值对应的特征向量以实现点云法向量的估算,利用MATLAB软件编程实现点云法向量估算。为可视化点云法向量,本文仅显示部分区域的点云法向量,选取区域的X,Y和Z范围分别为[-41,-21],[87,106]和[276,280],法向量可视化结果如图4所示。
图4
3.2 点云精简结果分析
3.2.1 K-means++聚类结果
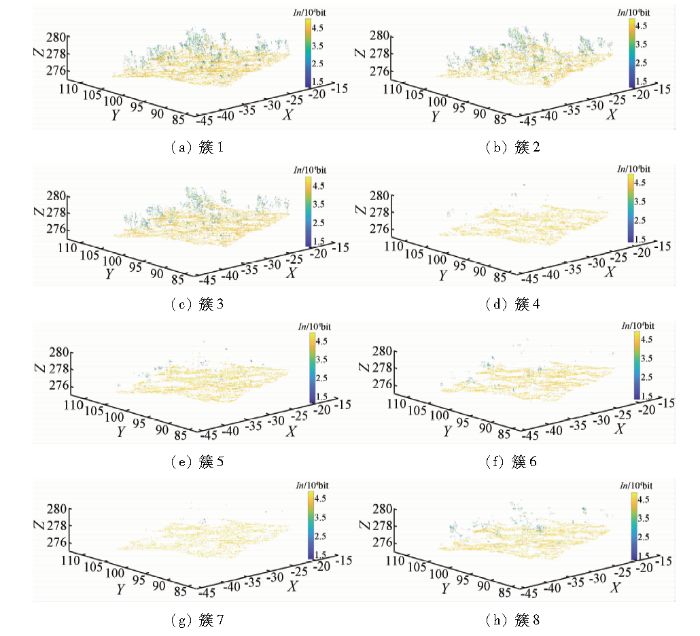
图5
图6
图6
K-means++对法向量聚类的三维可视化
Fig.6
3D visualization of K-means++ for clustering point cloud normal vector
对比聚类前后点云结果可知,簇1、簇2和簇3保持研究区地物特征,其他簇虽然很好地保存地形,但地物边界保留不完整。对聚类结果中点云个数和强度误差进行统计得到表4,分析表可知,因为簇2和簇3基本包含了研究区地物特征,所以对应的最小强度误差为0,且簇3强度误差范围最小,为87。结合聚类结果可视化和统计可知,按照精简率为81.389%,85.369%和81.833%进行点云精简处理比按照精简率为90.916%,88.300%,89.606%,94.031%,88.557%处理的效果更好,即点云越多更容易表达地物细节特征。
表4 聚类后点云个数和强度误差统计
Tab.4
| 类别 | 聚类后的 点云个数 | 点云精简 率/% | 点云回波强度误差 | |
|---|---|---|---|---|
| 最小误差 | 最大误差 | |||
| 簇1 | 11 506 | 81.389 | 437 | 787 |
| 簇2 | 9 045 | 85.369 | 0 | 961 |
| 簇3 | 11 231 | 81.833 | 0 | 87 |
| 簇4 | 5 616 | 90.916 | 677 | 2 534 |
| 簇5 | 7 234 | 88.300 | 437 | 612 |
| 簇6 | 6 426 | 89.606 | 524 | 2 469 |
| 簇7 | 3 690 | 94.031 | 1 224 | 1 551 |
| 簇8 | 7 074 | 88.557 | 852 | 918 |
3.2.2 点云精简分析
图7
图7
簇1、簇2和簇3对应点云的Delaunay三角网
Fig.7
Delaunay triangulation of clusters 1, clusters 2 and clusters 3
表5 聚类前后Delaunay三角网统计结果和相关系数
Tab.5
| 点云精简 率/% | 类别 | 三角网 数据/个 | 三角网顶 点数据/个 | 构建三角 网时间/s | 相关系数 |
|---|---|---|---|---|---|
| 81.389 | 簇1 | 22 983 | 11 505 | 0.28 | 0.884 |
| 85.369 | 簇2 | 18 061 | 9 044 | 0.32 | 0.870 |
| 81.833 | 簇3 | 22 434 | 11 230 | 0.23 | 0.890 |
| 100 | 聚类前 | 123 578 | 61 809 | 1.01 | 1 |
分析表5可知,采用精简后点云生成三角网时间大大缩短; 按照81.389%,85.369%和81.833%进行精简处理后的点云基本参与三角网的生成中; 当点云精简率为81.833%时,其对应的相关系数最高0.890,且运行时间最短,为0.23 s。
4 结论与讨论
1)利用肘方法可以较好地确定聚类数目; 同时,随机抽取点云作为初始中心,且独立运行聚类方法多次,结合聚类偏差定量选取最终聚类结果,较好地解决聚类两大问题。
2)通过KD树建立点云的数据结构,利用其构建点云的K邻域,且采用PCA方法估算法向量。最后利用K-means++聚类方法实现点云精简,精简率分别为81.389%,85.369%和81.833%。
3)通过生成Delaunay三角网,且转换为栅格数据,计算精简前后的相关系数。综合考虑运行时间和相关系数,可知点云精简率为81.833%时效果最好。
4)本文方法通过一次点云聚类处理即可获取不同精简率的点云,根据点云应用领域的不同可以随机选取不同的精简结果。本文方法的不足之处在于: 只关注K-means++聚类方法可以实现点云的精简处理,且验证精简结果,但在建立点云K邻域时,本文直接选择K=10,虽然可以提高邻域构建速度,但是对不同邻域K值的设定影响点云法向量的估算结果,需要进一步研究。
参考文献
无检校场的机载LiDAR点云数据检校方法
[J].
Calibration of airborne LiDAR cloud point data with no calibration field
[J].
High resolution hydric soil mapping using LiDAR digital terrain modeling
[J].
基于法向夹角的点云数据精简算法
[J].
Point cloud simplification based on angle between normal
[J].
A feature preserving algorithm for point cloud simplification based on hierarchical clustering
[C]//
一种散乱点云的均匀精简算法
[J].
An uniform simplification algorithm for scattered point cloud
[J].
散乱点云特征提取和聚类精简技术研究
[D].
Research on feature extraction and clustering simplification of scattered point cloud
[D].
基于曲率特征信息的散乱点云数据预处理技术研究
[D].
Research on data pre-processing technology of scattered point cloud based on curvatures feature
[D].
于法向量夹角信息熵的点云简化算法
[J].
Point cloud simplification based on the information entropy of normal vector angle
[J].
Point cloud simplification with preserved edge based on normal vector
[J].DOI:10.1016/j.ijleo.2015.05.092 URL [本文引用: 1]
基于K-means聚类的RGBD点云去噪和精简算法
[J].
Algorithm for RGBD point cloud denoising and simplification based on K-means clustering
[J].
三维点云数据精简与压缩的研究
[D].
Research on 3D point cloud data simplification and compression
[D].
Automatic evaluation of machining allowance of precision castings based on plane features from 3D point cloud
[J].
DOI:10.1016/j.compind.2013.06.003
URL
[本文引用: 1]

A novel automatic precision casting machining allowance evaluation approach, which is accomplished by a two-step rough-precise point cloud registration based on plane features extracted from the two point clouds (i.e. the measured precision casting point cloud and the point cloud discretized from the CAD model), is proposed in this paper. Firstly, the two point clouds are registered roughly by PCA algorithm. Secondly, an improved plane fitting and merging algorithm is proposed to extract the plane features from both the two point clouds. The extracted plane features are matched by searching the nearest plane feature description vector. The rotation matrix for the precise registration can then be derived by registering the normal vectors of the matched plane features. Finally, the machining allowance at each point is obtained by calculating the distance between the corresponding points along the normal direction. The experiment on precision casting machining allowance evaluation is given to show the performance of the proposed approach. (C) 2013 Elsevier B.V.
基于区域多次回波点密度分析的城区LiDAR建筑物提取
[J].以正确提取城区LiDAR点云中建筑物为目标,综合利用不同类别目标点云的回波特征以及地形信息,提出了一种基于区域多次回波密度分析的LiDAR点云建筑物提取方法。首先,将点云构建不规则三角网(triangulated irregular network,TIN),获取封闭的等高线; 然后,利用等高线间的拓扑关系得到等高线族区域; 最后,统计每一区域的多次回波点云密度信息,通过建筑物和树木区域多次回波点云在区域密度上的巨大差异来识别建筑物点云和树木点云。研究结果表明: 该方法既充分利用了建筑物表面与植被间多次回波特性的差异,又不否定建筑物边缘同样存在多次回波的现象; 通过封闭的等高线自适应地检测出地物目标的轮廓,弥补了传统LiDAR建筑物提取方法的不足; 该方法能够较其他方法更准确地提取建筑物。
Classification of LiDAR point clouds in urban areas based on the analysis of regional multi-return density
[J].
Occluded boundary detection for small-footprint ground borne LiDAR point cloud guided by last echo
[J].DOI:10.1109/LGRS.8859 URL [本文引用: 1]
Impact of normalization in distributed K-means clustering
[J].
基于特征融合的林下环境点云分割
[J].
Point cloud segmentation algorithm based on feature fusion used for understory environments
[J].
基于KD树散乱点云数据的Guass平均曲率精简算法
[J].
Guass mean curvature reduction algorithm based on KD tree scattered point cloud data
[J].
基于K近邻的点云数据处理研究
[D].
Research on point cloud data processing based on K-nearest neighbor
[D].
基于激光扫描的三维点云数据处理技术研究
[D].
Research on data processing techniques based on laser scanning 3D point clouds
[D].
基于栅格划分和法向量估计的点云数据压缩
[J].
Point cloud data compression based on grid division and normal vector estimation
[J].
自适应K-means聚类的散乱点云精简
[J].
Adaptive K-means clustering simplification of scattered point cloud
[J].
改进的K-means算法在遥感图像分类中的应用
[J].遥感图像分类时,如果类别不明,K-means算法随机选取不同初值会导致分类结果有较大的差异。针对此问题,提出了一种改进的K-means算法。首先对遥感数据进行对数变换; 然后采用主成分变换,依据主成分贡献率(≥85%)选择参与分类的主成分数; 根据第一主成分的概率密度函数确定初始分类数和初始分类中心,并确定初始分类标签作为多个主成分的期望最大化(EM)分类算法所需初始值,避开了随机选取初值的敏感问题。通过实验数据验证,本文方法的分类精度优于传统的基于均值-方差的K-means算法。
An improved K-means algorithm for remote sensing classification
[J].
最优聚类个数和初始聚类中心点选取算法研究
[J].
Application research of computers study on the optimal number of clusters and the selection algorithm of initial cluster centers
[J].
Seamless service handoff based on Delaunay triangulation for mobile cloud computing
[J].DOI:10.1007/s11277-014-2229-6 URL [本文引用: 1]